bonjour !j'ai un peu de mal avec les limites meme je peux dire que je comprends pas grand chose mais cet exercice la est essentiel enfin c'est ce que nous a dit notre prof de maths alors j'espere que vous pourrez m'aidez s'il vous plait ! voici l'énoncé :
on considere la fonction F>racine ( 25-4t²) définie sur I=[0;5/2]
on pose t(h)= [ F(3/2+h)-F(3/2)]/h (h differents de 0)
démontrer que T(h)=( 12-4h )/ racine de ( 16-12h-4h²) +4
b) en déduire que la fonction est derivable en 3/2
2) une barre [AB] a ses extremites qui coulissent sur les demi axes [Ox) et [oy) d'un repere orthonormal dont l'unité est 1 cm l'extremité A se déplace a une vitesse constante de 2cm .s-1 ! quelle vitesse instantanée de l'extremité B lorsque A est a 3 cm de O ! finit
la question 1 je l'ai faite mais la 2 je ne comprends pas ,
JE vous serai tres reconnaissant de m'aider , Merci :happy2:
Encore du barycentre
9 messages
- Page 1 sur 1
Soit l la longueur de la barre, et j'appelle x la longueur OA, y la longueur OB.
Alors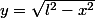 , et comme A se déplace à vitesse constante,
, et comme A se déplace à vitesse constante, 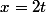 (en supposant que A est en O à l'instant 0, ce qui ne change rien).
(en supposant que A est en O à l'instant 0, ce qui ne change rien).
On a donc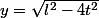 et donc
et donc 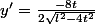 est la vitesse de B (on vire le signe - si on veut une vitesse absolue)
est la vitesse de B (on vire le signe - si on veut une vitesse absolue)
Comme A est à 3 cm de 0, on a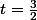
Alors
On a donc
Comme A est à 3 cm de 0, on a
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
