Polynomes

par **Clembou** » 22 Aoû 2008, 12:49

magnolia86 a écrit:
Comment-ça lesquelles ?
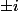
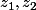
Pour toi, quand on écrit , on connaît mieux les racines de X²+1 que lorsqu'on les écrit ? Personnellement, je ne vois là que des symboles. :happy2: idem avec ...

C'est pourtant clair, pour moi, connaître un objet, c'est connaître ses propriétés, et en particulier des propriétés qui peuvent/vont servir après. Faut-il encore savoir ce qu'on veut faire après...

Je serais plus renseigné en disant que les racines de

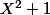
sont

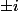
que

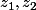
(parce que je connais la signification de

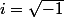
). Désolé mais me dire que les racines de tels polynômes sont

, je dis oui mais que vaut les

.

C'est ma dernière réponse à cette discussion totalement inutile :triste:

par **magnolia86** » 22 Aoû 2008, 13:19

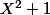
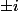
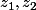
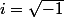
Clembou a écrit:Je serais plus renseigné en disant que les racines de sont que (parce que je connais la signification de ). Désolé mais me dire que les racines de tels polynômes sont , je dis oui mais que vaut les .

Je pense que tu n'as pas assez de recul sur le sujet.

Si

est racine de

, je pense bien que

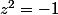
, comme ton

...

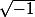
Regarde le nombre de démonstrations où on utilise l'existence de racines dans C, que l'on nomme simplement

, sans jamais les calculer sous quelque forme que se soient. Dans ces inombrables preuves, on arrive a faire quelque chose de ces

. C'est donc qu'on les connaît suffisamment pour conclure plein de chose. Merci le théorème de d'Alembert-Gauss !

Clembou a écrit:C'est ma dernière réponse à cette discussion totalement inutile :triste:

je comprends...

par **Nightmare** » 22 Aoû 2008, 14:35

Effectivement, après avoir écrit que

, il vaut mieux t'arrêter là la discussion :lol3:

par **miikou** » 22 Aoû 2008, 14:44

'Si quelqu'un peu me donner une technique qui marche pour tous cas afin de trouver les racines d'un polynome de degrés supérieur à 2'

tu risques d'attendre longtemps :ptdr:

clembou es tu certain de bien etre en licence ??

par **Black Jack** » 23 Aoû 2008, 15:53

magnolia86 a écrit:Est-ce que connaître une approximation numérique est moins intéressant que d'avoir une grosse expression algébrique avec radicaux tenant sur 3 lignes ? Est-ce qu'avoir une expression algébrique d'un nombre permet de mieux manipuler ce nombre ??

Ai-je dit cela ?

Ma réponse avait au moins d'intéressant de mentionner des méthodes analytiques possibles pour les degrés 3 et 4 et de préciser que ce n'était plus possible sauf cas spécial pour les degrés >= 5 (ce qui n'avait pas été été dit dans ce fil et répondait à la question initiale).

Et pour les degrés >= 5, sauf cas spécial, l'approche par approximations successives ou graphique est possible.
... Mais cela reste des approximations et pas toujours faciles à trouver surtout si on ne se cantonne pas dans R pour les racines.

Et l'utilité des approximations dépend évidemment de ce qu'on a à faire ...

Qu'est ce qui est dérangeant dans ma réponse ?

:zen:

par **leon1789** » 23 Aoû 2008, 16:11

Black Jack a écrit:Ma réponse avait au moins d'intéressant de mentionner des méthodes analytiques possibles pour les degrés 3 et 4 et de préciser que ce n'était plus possible sauf cas spécial pour les degrés >= 5 (ce qui n'avait pas été été dit dans ce fil et répondait à la question initiale).

En passant juste en coup de vent, ce ne sont pas des méthodes analytiques, mais algébriques (Ferrari, Cardan)

par **Black Jack** » 23 Aoû 2008, 16:27

On peut donc modifier ma réponse en :

Ma réponse avait au moins d'intéressant de mentionner des méthodes algébriques possibles pour les degrés 3 et 4 et de préciser que ce n'était plus possible sauf cas spécial pour les degrés >= 5 (ce qui n'avait pas été été dit dans ce fil et répondait à la question initiale).

...

:zen:

par **leon1789** » 23 Aoû 2008, 16:29

Black Jack a écrit: :zen:

tu peux le faire :ptdr:

par **leon1789** » 23 Aoû 2008, 16:30

Il existe une méthode avec des cosinus et sinus (je ne sais plus) pour résoudre les équations de degré 3. De degré

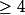
, je ne sais pas. Quelqu'un sait ?

par **Clembou** » 23 Aoû 2008, 16:41

miikou a écrit:
clembou es tu certain de bien etre en licence ??

C'est quoi cette attaque inutile ? :hum: Pourquoi tu me poses cette question dont tu sais déjà la réponse ?

par **Alpha** » 23 Aoû 2008, 16:50

Clembou a écrit:C'est quoi cette attaque inutile ? :hum: Pourquoi tu me poses cette question dont tu sais déjà la réponse ?

En effet, il s'agit là d'une attaque personnelle... Même en rigolant, mieux vaut éviter! La prochaine fois, miikou sera exclu temporairement.

Mais il faut (à mon avis) également éviter de dire sans bonnes raisons qu'une discussion est inutile.

Quoi qu'il en soit, que tout le monde garde son calme et passe à autre chose
:zen:

par **Clembou** » 23 Aoû 2008, 16:51

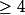
leon1789 a écrit:Il existe une méthode avec des cosinus et sinus (je ne sais plus) pour résoudre les équations de degré 3. De degré , je ne sais pas. Quelqu'un sait ?

Page Wikipedia : http://fr.wikipedia.org/wiki/%C3%89quation_polynomiale

par **leon1789** » 23 Aoû 2008, 17:12

Chacun voit midi à sa porte... et il est minuit (à Pékin !)

Clembou a écrit:Page Wikipedia : http://fr.wikipedia.org/wiki/%C3%89quation_polynomiale

Merci, j'ai regardé rapidement la page et les liens de cette page, mais je n'ai pas vu de méthode utilisant les fonctions trigonométriques. :triste:

par **Clembou** » 23 Aoû 2008, 17:15

leon1789 a écrit:Chacun voit midi à sa porte... et il est minuit (à Pékin !)

Merci, j'ai regardé rapidement la page et les liens de cette page, mais je n'ai pas vu de méthode utilisant les fonctions trigonométriques. :triste:

Oups ! J'ai lu trop vite alors :triste: Je ne connais pas cette méthode pour la recherche des racines polynomiales par fonctions trigonométriques.

Polynomes

Qui est en ligne