Polynomes

[Anonyme]

Bonjours à tous,
Je ne comprends pas très bien mes cours sur les polynomes c'est pourquoi j'ai besoin de vous.

Si quelqu'un peu me donner une technique qui marche pour tous cas afin de trouver les racines d'un polynome de degrés supérieur à 2 .

De même, pour décomoser un polynome en produit de polynomes irréductibles. dans C ou R.

J'ai un exemple que je n'arrive pas à résoudre :
Soit le polynome P(X)=X^3+X^2-2X-8
a) Montrer que P admet une racine et une seule , que l'on déterminera.
b) Décomposer P(X) en produit de polynômes irréductibles dans R puis dans C.

Merci d'avance.
PS : c'est la méthode qui m'interresse. et pas le simple corrigé de cet exercice.

[Nightmare]

Salut :happy3:

Que penser de P pour X=2 ?

[magnolia86]

Si quelqu'un peu me donner une technique qui marche pour tous cas afin de trouver les racines d'un polynome de degrés supérieur à 2 .

Une technique algébrique, numérique, avec trigo, avec radicaux, via de l'analyse, ... ?

[Anonyme]

merci, X = 2 m j'avais trouvé :id:
et décomposer en polynome irréductible ??
Et quand je parle d'un technique pour trouver les racines d'un polynome, peu mimporte sur la façon tant que ça fonctionne pour tout les polynomes.
Je veux juste une technique général.
merci...

[Clembou]

merci, X = 2 m j'avais trouvé :id:
et décomposer en polynome irréductible ??
Et quand je parle d'un technique pour trouver les racines d'un polynome, peu mimporte sur la façon tant que ça fonctionne pour tout les polynomes.
Je veux juste une technique général.
merci...

Si 2 est racine de ton polynôme, ce polynôme sera de la forme :



avec a,b,c à définir en développant l'expression simplifié...

[magnolia86]

Et quand je parle d'un technique pour trouver les racines d'un polynome, peu mimporte sur la façon tant que ça fonctionne pour tout les polynomes.
Je veux juste une technique général.

Une technique super générale qui permet de "connaitre" les racines d'un polynôme ?

hummm dans C (bien assez général, quoi que...), j'utiliserais le théorème de D'Alembert-Gauss, et comme ça on obtient les n racines d'un polynôme de degré n : z_1,...,_z_n.

--> Il faudrait au minimum que tu dises à quoi vont te servir les racines des polynômes :id:

[Nightmare]

magnolia86 : Tu arrives à utiliser d'Alembert-Gauss pour trouver des racines? Il faut que tu me montres comment :happy3:

[Black Jack]

Il existe des techniques pour trouver les racines de polynôme jusqu'au 4ème degré.

Par exemple : Méthode de Cardan pour le degré 3 et Methode de Ferrari pour le degré 4.

Ces méthodes permettent de trouver les racines dans tous les cas, pas besoin qu'il s'agisse de polynômes spéciaux comme les bicarrés ou a coefficients palyndromes ou autres.

A partir du degré 5 et plus haut, sauf cas spéciaux de racine(s) évidente(s), il n'existe plus de méthodes analytiques.

On peut évidemment trouver certaines solutions par approximations successives ou bien graphiquement, mais ce ne sont évidemment que des approximations.

:zen:

[magnolia86]

magnolia86 : Tu arrives à utiliser d'Alembert-Gauss pour trouver des racines? Il faut que tu me montres comment :happy3:

Le théorème dit que tout polynôme P de degré n possède n racines dans C. Voilà, j'ai trouvé toutes les racines de P dans C et je peux jouer avec : par exemple leur produit vaut P(0) . :ptdr:


Ce que je veux dire depuis le début, c'est que les verbes "trouver les racines" ou "connaitre les zéros" sont trop vagues pour qu'une réponse précise soit donnée.

D'ailleurs, avoir sous les yeux les 20 premières décimales de , est-ce connaitre ? Savoir que et , est-ce connaître ? Bref, que signifie "connaître" ???

[magnolia86]

Il existe des techniques pour trouver les racines de polynôme jusqu'au 4ème degré.

Par exemple : Méthode de Cardan pour le degré 3 et Methode de Ferrari pour le degré 4.

Ces méthodes permettent de trouver les racines dans tous les cas, pas besoin qu'il s'agisse de polynômes spéciaux comme les bicarrés ou a coefficients palyndromes ou autres.

A partir du degré 5 et plus haut, sauf cas spéciaux de racine(s) évidente(s), il n'existe plus de méthodes analytiques.

A partir du degré 5 et plus haut, sauf cas spéciaux de racine(s) évidente(s), il n'existe plus de méthodes ... exprimant les racines avec des radicaux ! (Edit : et en plus, c'est plus compliqué que ça)

On peut évidemment trouver certaines solutions par approximations successives ou bien graphiquement, mais ce ne sont évidemment que des approximations.
:zen:

Est-ce que connaître une approximation numérique est moins intéressant que d'avoir une grosse expression algébrique avec radicaux tenant sur 3 lignes ? Est-ce qu'avoir une expression algébrique d'un nombre permet de mieux manipuler ce nombre ??

Approximation numérique, écriture par radicaux, etc. une bonne méthode pour "connaître" les racines dépend de ce qu'on veut faire de ces racines. :we:

[Nightmare]

Bof... Au final tu t'embrouilles plus qu'autre chose. La réponse de Black Jack était adaptée à la question, le topic aurait dû s'arrêter là.

[Clembou]

Le théorème dit que tout polynôme P de degré n possède n racines dans C. Voilà, j'ai trouvé toutes les racines de P dans C et je peux jouer avec : par exemple leur produit vaut P(0) . :ptdr:


Ce que je veux dire depuis le début, c'est que les verbes "trouver les racines" ou "connaitre les zéros" sont trop vagues pour qu'une réponse précise soit donnée.

D'ailleurs, avoir sous les yeux les 20 premières décimales de , est-ce connaitre ? Savoir que et , est-ce connaître ? Bref, que signifie "connaître" ???

Je veux bien que tu sais que si un polynôme dans C est de degré n alors il a n racines mais encore faut-il savoir lesquelles ? :triste:

[Doraki]

Comme l'a dit magnolia, "savoir lesquelles" est une notion assez vague.
Ca dépend vraiment de ce que tu veux en faire plus tard.

Par exemple tu pourrais essayer les formules de Cardan sur l'exemple du sujet je suis pas sur que tu puisses identifier la racine 2 très facilement à la fin.

[magnolia86]

Bof... Au final tu t'embrouilles plus qu'autre chose. La réponse de Black Jack était adaptée à la question, le topic aurait dû s'arrêter là.

Je ne m'embrouilles pas, au contraire j'ai une certaine expérience en la matière... Et j'invite 7180 a réfléchir à la question qu'il pose.

Je veux bien que tu sais que si un polynôme dans C est de degré n alors il a n racines mais encore faut-il savoir lesquelles ?

Comment-ça lesquelles ?
Pour toi, quand on écrit , on connaît mieux les racines de X²+1 que lorsqu'on les écrit ? Personnellement, je ne vois là que des symboles. :happy2: idem avec ...

C'est pourtant clair, pour moi, connaître un objet, c'est connaître ses propriétés, et en particulier des propriétés qui peuvent/vont servir après. Faut-il encore savoir ce qu'on veut faire après...

[Nightmare]

magnolia86 > Je ne dit pas que je ne suis pas d'accord avec toi, bien que je ne le sois pas totalement.

Je suis d'accord lorsque tu dis que donner un symbole à une solution, ce n'est pas réellement la connaître. Cependant, au fil de l'évolution des mathématiques, on a appris les propriétés de ces symboles (e, i, , 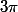etc...).

Aussi, au jour d'aujourd'hui, c'est beaucoup plus parlant de savoir qu'une solution d'une équation est plutôt que 2.4142... (en terme mathématique je parle, en terme physique et pratique c'est useless comme disent nos amis anglosaxons)

[magnolia86]

Bof... Au final tu t'embrouilles plus qu'autre chose. La réponse de Black Jack était adaptée à la question, le topic aurait dû s'arrêter là.

Je ne m'embrouilles pas, au contraire j'ai une certaine expérience en la matière...

Et j'invite 7180 a réfléchir à la question qu'il pose.

Je veux bien que tu sais que si un polynôme dans C est de degré n alors il a n racines mais encore faut-il savoir lesquelles ?

Comment-ça lesquelles ?
Pour toi, quand on écrit , on connaît mieux les racines de X²+1 que lorsqu'on les écrit ? Personnellement, je ne vois là que des symboles. :happy2: idem avec ...

C'est pourtant clair, pour moi, connaître un objet, c'est connaître ses propriétés, et en particulier des propriétés qui peuvent/vont servir après. Faut-il encore savoir ce qu'on veut faire après...

[magnolia86]

magnolia86 > Je ne dit pas que je ne suis pas d'accord avec toi, bien que je ne le sois pas totalement.

ok, on ne peut être à 100% d'accord sur tout :we:

Aussi, au jour d'aujourd'hui, c'est beaucoup plus parlant de savoir qu'une solution d'une équation est plutôt que 2.4142... (en terme mathématique je parle, en terme physique et pratique c'est useless comme disent nos amis anglosaxons)

As-tu idée de la manière dont les ordinateurs calculent (très bien !) avec les nombres algébriques ? Certainement pas avec des radicaux...

[Nightmare]

Pourquoi me parles-tu d'ordinateur? Ce que j'ai mis entre parenthèse n'était pas censé être transparent!

Ce que je te dis c'est que si l'on veut étudier une solution, c'est beaucoup plus parlant de l'avoir sous sa forme formelle. Etudier une approximation c'est inutile.

Maintenant, et c'est là où je suis d'accord avec toi, si je te dis que mon pendule a une période de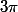 , dans la pratique c'est inutile, car j'en ai rien à faire que la période de mon pendule annule la fonction sinus :lol3:

[magnolia86]

Ok avec toi.

Ce que je te dis c'est que si l'on veut étudier une solution, c'est beaucoup plus parlant de l'avoir sous sa forme formelle. Etudier une approximation c'est inutile.

...mais des "formes formelles", il y en a des paquets. Certaines peuvent être plus adaptées en fonction de la suite qu'on veut donner.

[Nightmare]

Certaines peuvent être plus adaptées en fonction de la suite qu'on veut donner.

Oui, voila là où nos opinions convergent. Au final tout est une question de contexte, en l'occurrence ici il n'y en avait pas, donc toute réponse était possible :lol3: