Montrer qu'une fonction est continue

[rads]

Bonjour .J'essaie de faire cet exo depuis ce mat mais j'arrive a rien
Voici l'enoncé :
f(x)=E(x) + [x+E(x)]²
1) montrer que f est continue en tout point x0 appartenant à R.
2)calculer limf(x)/x (x tend vers +inf)

J'espere que vous serez plus inspire que moi.

[xyz1975]

Bonjour,
Est ce que vous connaissez les propriètés de la fonction partie entière?

[magnolia86]

L'énoncé, ce n'est pas avec f(x)=E(x) + [x-E(x)]² plutôt ?

[rads]

oui mais je ne ssais pas comment faire pour montrer qu'une telle fonction est continue

[rads]

L'énoncé, ce n'est pas avec f(x)=E(x) + [x-E(x)]² plutôt ?

Oui c'es bien f(x)=E(x) + [x-E(x)]² je me suis trompe en recopiant .merci

[Imod]

Il faut remarquer que f est un polynôme sur chaque intervalle [n;n+1[ avec n entier , il reste alors à étudier la continuité de f à gauche de chaque entier .

Imod

[rads]

Il faut remarquer que f est un polynôme sur chaque intervalle [n;n+1[ avec n entier , il reste alors à étudier la continuité de f à gauche de chaque entier .

Imod

J'avoue que je ne comprend plus a partir de il reste à etudier..
Est que je dois encadrer chaque entier et utiliser le theoreme des gendarmes pour trouver la limite

[Imod]

Peux-tu dire à quoi est égale f sur [n;n+1[ et la valeur de f(n+1) ?

Imod

[rads]

Peux-tu dire à quoi est égale f sur [n;n+1[ et la valeur de f(n+1) ?

Imod

sur [n;n+1[ f = 4x²-3x+1
Je ne sais pas comment faire pour trouver lavaleur de f(n+1)

[Imod]

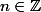
Il me semble qu'il faudrait déjà que tu te poses la question suivante : si avec , que vaut ?

Imod

[rads]

Finalement j'ai reussi à le faire avec l'aide de mon prof de math . J'avais completent oublié qu'il fallait donner l'expression de E(x) avant de calculer sa limite. Il fallait donc donner l'expression de E(x) si x appartient à R et si x appartient à Z et comparer la limite de f dans ces deux cas et conclure.
Merci de l'aide que vous m'avez fournie

[Imod]

Sympa de remercier , j'en connais pour qui ce n'est pas tout à fait naturel :++:

Imod