Runge Kutta
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 20 Aoû 2008, 15:32
par aure555 » 20 Aoû 2008, 15:32
Bonjour,
j'ai une question concernant runge kutta d'ordre 4.
Dans le processus d'itération, on utilise une fonction f mais comment trouver cette fonction?
 = f(t,u(t)) \\ u(t_o) = u_0)
Je ne vois pas comment retrouver la fonction.
Prenons par exemple
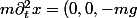 + E + P)
Je n'arrive pas à voir dans cette équation la fonction f qu'il faudra pour commencer runge kutta...
Merci de votre aide
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 15:53
par magnolia86 » 20 Aoû 2008, 15:53
Que comprends-tu de cette équation
 = f(t,u(t)))
? peux-tu nous dire en français ce qu'elle signifie pour toi ?
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 20 Aoû 2008, 16:12
par aure555 » 20 Aoû 2008, 16:12
Il faut trouver la fonction u(t) tel que en la dérivant, on obitent la fonction de droite f(t,u(t)) et donc cette dernière utilise dans son expression t et u(t)...
Je me rends compte que je n'arrive pas à poser clairement des mots dessus finalement
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 20 Aoû 2008, 16:38
par Maxmau » 20 Aoû 2008, 16:38
aure555 a écrit:Bonjour,
j'ai une question concernant runge kutta d'ordre 4.
Dans le processus d'itération, on utilise une fonction f mais comment trouver cette fonction?
 = f(t,u(t)) \\ u(t_o) = u_0)
Je ne vois pas comment retrouver la fonction.
Prenons par exemple
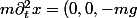 + E + P)
Je n'arrive pas à voir dans cette équation la fonction f qu'il faudra pour commencer runge kutta...
Merci de votre aide
Bonjour
La méthode RK4 est impossible à exposer ici
Elle est utilisée pour résoudre numériquement une équation différentielle :
u = f(t,u) ; u(t0) = u0 où u(t) est la fonction inconnue
par exemple : u = t + u ; u(0) = 1
Dans cet exemple : f(t,u) = t+u
Cherche lalgorithme RK4 sur le net (sur Wikipedia par exemple)
Cet algorithme est très pénible à justifier
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 17:36
par magnolia86 » 20 Aoû 2008, 17:36
aure555 a écrit:Il faut trouver la fonction u(t) tel que en la dérivant, on obtient la fonction de droite f(t,u(t)) et donc cette dernière utilise dans son expression t et u(t)...
ok.
Tu as remarqué que dans ton exemple
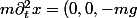 + E + P)
, c'est la dérivée seconde qui rentre en jeu ?
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 17:37
par magnolia86 » 20 Aoû 2008, 17:37
Maxmau a écrit:Dans cet exemple : f(t,u) = t+u
Dans quel exemple ???
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 17:42
par magnolia86 » 20 Aoû 2008, 17:42
Maxmau a écrit:Cet algorithme est très pénible à justifier
Si j'ai de bons souvenirs, on peut le faire avec DL à deux variables. C'est un peu fastidieux à la main, mais à l'aide d'un ordi pour faire les calculs, le principe est assez simple. D'ailleurs, on peut trouver soi-même d'autres coefficients que ceux de RK4 et qui fonctionnent très bien également.
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 20 Aoû 2008, 18:29
par aure555 » 20 Aoû 2008, 18:29
magnolia86 a écrit:ok.
Tu as remarqué que dans ton exemple
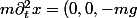 + E + P)
, c'est la dérivée seconde qui rentre en jeu ?
oui oui je l'ai remarqué
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 19:08
par magnolia86 » 20 Aoû 2008, 19:08
aure555 a écrit:oui oui je l'ai remarqué
et donc ton exemple ne rentre pas dans le cadre de la méthode RK4.
C'est normal que tu ne trouves pas le fonction f pour ton exemple.
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 20 Aoû 2008, 20:29
par aure555 » 20 Aoû 2008, 20:29
Ah ok daccord
Aurais-tu un exemple en tête à me montrer comment trouver cette fonction?
Merci pour tout
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 20:31
par magnolia86 » 20 Aoû 2008, 20:31
On peut reprendre l'exemple de Maxmau.
par exemple : y(t) = t + y(t) ; y(0) = 1
Dans cet exemple : f(t,u) = t+u
En effet f(t, y(t)) = t+y(t) = y'(t) .
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 20 Aoû 2008, 20:49
par xyz1975 » 20 Aoû 2008, 20:49
magnolia86 a écrit:On peut reprendre l'exemple de Maxmau.
En effet f(t, y(t)) = t+y(t) = y'(t) .
--------------------------------------------
--------------------------------------------
--------------------------------------------
---------------------------------------
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 20 Aoû 2008, 21:56
par magnolia86 » 20 Aoû 2008, 21:56
xyz1975 a écrit:--------------------------------------------
--------------------------------------------
--------------------------------------------
---------------------------------------
oula, ça c'est un message codé ou je ne m'y connais pas ! :ptdr:
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 20 Aoû 2008, 22:20
par xyz1975 » 20 Aoû 2008, 22:20
magnolia86 a écrit:oula, ça c'est un message codé ou je ne m'y connais pas ! :ptdr:
je l'ai effacé avant que Mr le modérateur Dominique Lefebre m'envoie des insultes bien décorées.
 par Dominique Lefebvre » 20 Aoû 2008, 22:28
par Dominique Lefebvre » 20 Aoû 2008, 22:28
xyz1975 a écrit:je l'ai effacé avant que Mr le modérateur Dominique Lefebre m'envoie des insultes bien décorées.
Des insultes !! Non, simplement un rappel au règlement .... Et je te signale que tu as la possibilité de supprimer un message, ce qui serait sans doute préférable à cet alignement de pointillés!
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 20 Aoû 2008, 22:30
par xyz1975 » 20 Aoû 2008, 22:30
Dominique Lefebvre a écrit:Et je te signale que tu as la possibilité de supprimer un message, ce qui serait sans doute préférable à cet alignement de pointillés!
ça je l'ignore, moi et l'informatique ça fait 37000, j'aimerais bien savoir comment.
 par Dominique Lefebvre » 20 Aoû 2008, 22:32
par Dominique Lefebvre » 20 Aoû 2008, 22:32
xyz1975 a écrit:ça je l'ignore, moi et l'informatique ça fait 37000, j'aimerais bien savoir comment.
Tu cliques sur le bouton Modifier en bas à droite de ton message. Et tu auras l'option de le supprimer...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
