Equation complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 17 Aoû 2008, 21:08
par xyz1975 » 17 Aoû 2008, 21:08
kasoo a écrit:Bien sur avec 2 équations du type
ax+by=c
dx+ey=f
les solutions peuvent facilement être trouvées
Mais avec 2 équations comme celle de l'exo :
ax+by=c
dxy=e
on ne peut pas conclure de la même façon, il ya beaucoup plus de solutions, ici il y a une équation supplémentaire qui limite les solutions.
Qu'on me corrige si je me trompe (ce qui est possible ^^)
On montre facilement que les deux systèmes sont équivalents "logiquement" donc ils possèdent le même ensemble de solutions, la troisième ne limite pas les solutions (et pourquoi limiter) par contre elle simplifie la résolution.
x²-y²=1....(1)
2xy=1......(2)
(2) est équivalente à x=

(on sait que y est non nul sinon le produit ne donne pas 1.
Il suffit alors de remlacer dans (1) on tombe sur une équation de degré 4 (bicarrée) il suffit dans ce cas de faire un changement d'inconnue.
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 17 Aoû 2008, 21:18
par john david » 17 Aoû 2008, 21:18
Cet exercice est présenté comme un exo de révision avant la 1ere année de PCSI.
Merci de votre aide pour cette question voilà mes résultats finaux avec lesquels je retombe sur mes pattes si mes calculs sont justes :
x = + ou - rac ( rac (2)+ 1 ) / rac 2
x = + ou - rac ( rac (2)- 1 ) / rac 2
y = + ou - 1 / rac ( 2 rac (2) + 2 )
y = + ou - 1 / rac ( 2 rac (2) - 2 )
C'est encore un peu fouilli la manière dont j'ai réussi à trouver cela mais je vais y réfléchir pendant la nuit ;)
J'espère avoir juste et si c'est bien le cas merci tout le monde :)
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:24
par magnolia86 » 17 Aoû 2008, 21:24
nuage a écrit:Il est alors facile de trouver

et
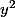
comme racines d'une équation du second degré.
A une résolution d'une équation de degré 2, je préfère une astuce (certes, ce n'est qu'une astuce) qui me donne instantanément les valeurs de x² et y² via 1 somme et 1 différence, mais c'est une question de goût.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:25
par magnolia86 » 17 Aoû 2008, 21:25
john david a écrit:x = + ou - rac ( rac (2)+ 1 ) / rac 2
x = + ou - rac ( rac (2)- 1 ) / rac 2
y = + ou - 1 / rac ( 2 rac (2) + 2 )
y = + ou - 1 / rac ( 2 rac (2) - 2 )
les + ou - sont totalement indépendants ? tu as 2 ou 2x2 = 4 solutions ?
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 17 Aoû 2008, 21:27
par xyz1975 » 17 Aoû 2008, 21:27
john david a écrit:x = + ou - rac ( rac (2)+ 1 ) / rac 2
x = + ou - rac ( rac (2)- 1 ) / rac 2
y = + ou - 1 / rac ( 2 rac (2) + 2 )
y = + ou - 1 / rac ( 2 rac (2) - 2 )
Plutot
Si

alors y=........
et
Si
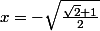
alors y=....
Voilà une défaillance du nouveau programme lorsqu'on a fait sauter l'algébre du programme du collège et evidemment du lycée, les solutions sont des couples (x;y) comme les coordonnées d'un point car la résolution se fait dans IR².
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 17 Aoû 2008, 21:28
par john david » 17 Aoû 2008, 21:28
Voilà xyz1975 a bien résumé la chose mais j'ai 4 valeurs de x possibles
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:29
par magnolia86 » 17 Aoû 2008, 21:29
Parfait ! :++: (mais j'ai pas vérifié les calculs...)
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 21:32
par magnolia86 » 17 Aoû 2008, 21:32
john david a écrit: j'ai 4 valeurs de x possibles
heu... c'est pô possible normalement.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 17 Aoû 2008, 21:55
par nuage » 17 Aoû 2008, 21:55
Salut,
Sinon, en fin de terminale le plus simple est peut-être de passer sous forme exponentielle :
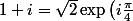)
d'où
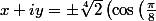 +i \sin\left(\frac{\pi}{8}\right)\right))
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 17 Aoû 2008, 22:20
par xyz1975 » 17 Aoû 2008, 22:20
nuage a écrit:Salut,
Sinon, en fin de terminale le plus simple est peut-être de passer sous forme exponentielle :
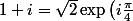)
d'où
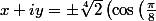 +i \sin\left(\frac{\pi}{8}\right)\right))
Erreur impardonnable d'où vient le pi/8??? On n'est pas dans IR
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 22:33
par magnolia86 » 17 Aoû 2008, 22:33
xyz1975 a écrit:Erreur impardonnable d'où vient le pi/8??? On n'est pas dans IR
le pi/8 vient de

: "argument" de la racine carrée.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 17 Aoû 2008, 22:34
par nuage » 17 Aoû 2008, 22:34
xyz1975 a écrit:Erreur impardonnable d'où vient le pi/8??? On n'est pas dans IR
Je te pardonne, mais tu devrais quand même savoir qu'un argument d'un produit est la somme des arguments des facteurs.
Donc si
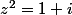
deux fois un argument de

est égal à

D'où l'idée de prendre
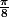
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 17 Aoû 2008, 22:50
par xyz1975 » 17 Aoû 2008, 22:50
nuage a écrit:Je te pardonne, mais tu devrais quand même savoir qu'un argument d'un produit est la somme des arguments des facteurs.
Donc si
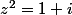
deux fois un argument de

est égal à

D'où l'idée de prendre
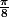
1/ J'ai pas dit que c'est faux mais je veux vous expliquer qu'il ne faut jamais manipuler la racine come dans IR, la fonction racine définie sur C est une fonction multiforme ce qui montre qu'on n'a pas le droit de composer avec elle lors de la recherche des solutions d'une équation tupe z^n=a si n est pair.
2/ Deux complexes sont égaux si et seulement si leurs modules sont égaux et leurs arguments sont égaux
modulo 2piSi on note

un argument de z si z²=1+i alors
2
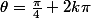
avec
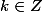
Donc
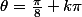
On remplace k par deux valeurs relatives consécutives pour trouver deux représentants des solutions.
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 18 Aoû 2008, 10:27
par john david » 18 Aoû 2008, 10:27
Mes résultats sont ils bons alors ?
J'ai essayé de passer par l'équation bicarrée et le changement de variable mais je ne retombe pas sur les même valeurs.
Quelqu'un pourrait il confirmer mes résultats pour que je puisse continuer mon exercice sereinement ? :D
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 18 Aoû 2008, 10:47
par john david » 18 Aoû 2008, 10:47
kasoo a écrit:Il me semble que mod(x+iy)²=x²+y² et non
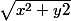
Donc l'équation donnée par les modules devient

ce qui expliquerait la difficulté à conclure
Me trompe-je ?
J'aurai tendance à dire que cela est faux.
Je m'explique.
Le module d'un complexe est égal à la racine de la somme des parties réelle et imaginaire du complexe élevées au carré.
Or ici le complexe est (x+iy)²
la partie réelle de ce complexe n'est pas x mais x²-y² !
et la partie imaginaire est 2xy
le module serait donc
rac ( (x²-y²)² + 4x²y² )
Non ?
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 18 Aoû 2008, 10:50
par xyz1975 » 18 Aoû 2008, 10:50
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 18 Aoû 2008, 10:52
par john david » 18 Aoû 2008, 10:52
Tu as trouvé cela en utilisant le fait que x²+y² = rac 2 ?
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 18 Aoû 2008, 10:53
par xyz1975 » 18 Aoû 2008, 10:53
john david a écrit:Tu as trouvé cela en utilisant le fait que x²+y² = rac 2 ?
On est d'accord pour la valeur de x, comme 2xy=1 soit alors y=1/(2x) on trouvera alors la valeur correspondante de y.
-
john david
- Membre Naturel
- Messages: 24
- Enregistré le: 17 Aoû 2008, 14:44
-
 par john david » 18 Aoû 2008, 11:03
par john david » 18 Aoû 2008, 11:03
En effet mais la valeur de x sur laquelle nous sommes ( mais je devrais dire étions ) d'accord je l'ai trouvé grace aux l'équations x²+y² = rac 2 et x² - y² = 1 or je viens de remettre en cause la validité de l'équation des modules ;)
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 18 Aoû 2008, 11:05
par xyz1975 » 18 Aoû 2008, 11:05
john david a écrit:or je viens de remettre en cause la validité de l'équation des modules

Pourquoi? elle reste valable, regardez l'un des messages où j'ai mis un système à 3 équations et travailler avec, laissez tomber l'équation bicarrée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
