Somme de 4 carrés
Olympiades mathématiques, énigmes et défis
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Aoû 2008, 17:52
par Imod » 17 Aoû 2008, 17:52
Comment résoudre ce petit problème au niveau lycée ( donc éviter les
:triste: ) .
Soient a , b , c , d , quatre entiers avec ab=cd , a²+b²+c²+d² peut-il être premier ?
Amusez-vous bien !!!
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 19:02
par lapras » 17 Aoû 2008, 19:02
Non il est toujours composé !
(factorisation toute bête)
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Aoû 2008, 19:09
par Imod » 17 Aoû 2008, 19:09
lapras a écrit:factorisation toute bête
Mais encore ?
Imod
-
IPCST
- Membre Naturel
- Messages: 12
- Enregistré le: 17 Aoû 2008, 16:54
-
 par IPCST » 17 Aoû 2008, 19:14
par IPCST » 17 Aoû 2008, 19:14
-
IPCST
- Membre Naturel
- Messages: 12
- Enregistré le: 17 Aoû 2008, 16:54
-
 par IPCST » 17 Aoû 2008, 19:15
par IPCST » 17 Aoû 2008, 19:15
(\alpha^{2}+\beta^{2}+ \gamma^{2}+\delta^{2})=(A^{2}+B^{2}+C^{2}+D^{2}))
avec
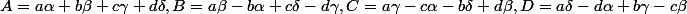
précisions :
si a=b=c= , d=1 ( par exemple ) , on ne peut avoir AB=CD
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 19:21
par miikou » 17 Aoû 2008, 19:21
imod on peut factoriser par ab
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 17 Aoû 2008, 19:24
par nodgim » 17 Aoû 2008, 19:24
La seule forme impaire de la somme de ces 4 carrés est 2^2k+a^2j+2^(2k-2i)+ a^2j*2^2i, a étant impaire.
Or, on peut voir dans cette somme la factorisation:
(2^2i +1)(a^2j+2^(2k-2i))
:id:
-
IPCST
- Membre Naturel
- Messages: 12
- Enregistré le: 17 Aoû 2008, 16:54
-
 par IPCST » 17 Aoû 2008, 19:24
par IPCST » 17 Aoû 2008, 19:24
Soit
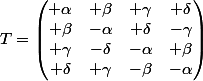
DONC
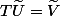
avec
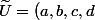)
et
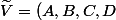)
Dans
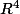
on a :
})^{2}.(\parallel\widetilde{U}\parallel)^2=(\parallel\widetilde{V}\parallel)^{2})
et comme
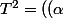^{2}+(\beta)^{2}+( \gamma)^{2}+(\delta)^{2}).I_{4})
on a :
(\alpha^{2}+\beta^{2}+ \gamma^{2}+\delta^{2})=(A^{2}+B^{2}+C^{2}+D^{2}))
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 17 Aoû 2008, 19:32
par miikou » 17 Aoû 2008, 19:32
heu xD plus modestement
a²+b²+c²+d² = (a-b)² + (c-d)² + 4 ab
soit ab est impaire, dans ce cas (a-b)² pair on conclus directement
soit ab pair
si a et b sont pairs (a-b)² aussi on conclus
si a pair et b impaire => (a-b)² impaire
donc (d-c)² impaire, en sommant (a-b)²+ (c-d)² +4ab est pair
ce qui conclus ( on traite le cas trivial 2 a part )
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Aoû 2008, 19:45
par lapras » 17 Aoû 2008, 19:45
Heureusement qu'on a dit niveau lycée !
a/c = d/b = x/y
 = 1)
=>
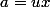
,
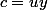
,
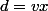
,
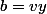
donc
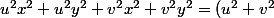(x^2 + y^2))
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 17 Aoû 2008, 19:50
par abcd22 » 17 Aoû 2008, 19:50
On suppose ab = cd non nul ou pas ?
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
 par magnolia86 » 17 Aoû 2008, 20:14
par magnolia86 » 17 Aoû 2008, 20:14
abcd22 a écrit:On suppose ab = cd non nul ou pas ?
C'est en quelque sorte la réponse à la question d'Imod
a²+b²+c²+d² peut-il être premier ?
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Aoû 2008, 20:20
par Imod » 17 Aoû 2008, 20:20
Beaucoup de réponses :zen:
J'attendais celle de Lapras ( interprétation géométrique ? ) avec la réserve de abc22 pour être complet .
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités