Démonstration de théorème de diagonalisation

[Daimios]

Bonjour à tous !

En préparation d'un examen, je cherche à démontrer ceci :

"Toute matrice qui peut être diagonalisée au moyen d'une matrice orthogonale
est nécessairement symétrique."

J'ai tenté par des calculs de trouver un lien explicable entre l'orthogonalité de la matrice B diagonalisant A, mais je tourne en rond.. Quelqu'un pourrait il m'éclairer sur cette démonstration ?

Merci d'avance

[nonam]

Bonjour.
Le fait pour une matrice M d'être diagonalisable au moyen d'une matrice orthogonale s'exprime par : il existe D diagonale et O orthogonale telles que :
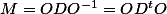(car O orthogonale).

Il suffit de calculer à l'aide de cette expression, et tu trouveras facilement que 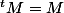(en utilisant les propriétés de base de la transposition, et la symétrie de D)