[aure555]

Bonjour,
j'ai une question concernant les hypothèses pour la méthode de la sécante.

J'ai été voir sur wikipédia et il est dit que la fonction f doit être 2 fois continuement différentiable et ce doit être une racine simple.

Il est aussi préférable que les valeurs initiales et soient suffisamment proches de la solution.

Au cour, on nous a donné ceci :

Soit f où ]a,b[ est un zéro simple de f. Posons = et

Supposons que > 0 soit suffisamment petit pour que ]a,b[ et < 1.

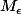
J'ai du mal a interpréter le . Quel est son rôle dans les hypothèses?

Merci d'avance

[leon1789]

Je ne sais pas si je vais pouvoir te répondre, mais j'ai quelques remarques préliminaires sur la méthode de la sécante : les hypothèses que tu signales ne suffisent pas pour assurer l'existence même de tous les termes de la suite. En effet, rien ne dit que f(x_n) et f(x_{n-1}) ne seront pas trop proches pour ne pas créer des problèmes dans la formule.

Reprenons l'exemple de wikipédia http://fr.wikipedia.org/wiki/M%C3%A9thode_de_la_s%C3%A9cante

On veut approximer la racine simple de dans l'intervalle [0,1] :
si on pose x_0 = 0 et x_1 = 1 alors il vient x_2 = 0.685... , x_3 = 0.841...
si on pose x_0 = 1 et x_1 = 0 alors il vient x_2 = 0.685... , mais x_3 = 1.252... On voit que x_3 quitte l'intervalle [0,1] du problème posé !

Donc je crois que l'étude de convergence sous-entend que tous les termes de la suite sont bien définis.

[leon1789]

Coté convergence :
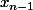
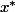
Si et sont proches (approximatif comme énoncé) de la racine simple de f, alors
où .
On obtient ça avec un développement de Taylor de .

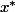
Ce résultat est juste sous condition que n'annule pas .

Ton résultat n'est plus très loin maintenant :we: