bombastus a écrit:Bon au moins tout le monde est d'accord sur la conclusion, c'est déjà ça!
Oui, on est tous d'accord sur le fait que 0 et

ne sont pas égaux.
Le problème ici est d'identifier l'erreur de raisonnement qui conduit au pseudo-paradoxe.
bombastus a écrit:Ce qui me gêne, ce sont les notations utilisées (avec pointillé),
exactement ! c'est là le hic de la démo, c'est le passage aux pointillés, c'est-à-dire le passage à l'infini. Des sommes finies de termes comme 1-1+2-2 ou 1-1+2-2+3 ne posent pas de problème : elle se calculent très bien.
Mais quand on passe à des sommes infinies de termes (des séries) alors il faut faire très attention : il y a des théorèmes pour cela. Souvent les théorèmes sur les séries supposent que celles-ci sont convergentes. Là on utilise un théorème de ce genre (regroupement par paquets), mais avec une séries non convergente, d'où le hic en réalité.
bombastus a écrit:si on écrit comme tu l'as fait leon:
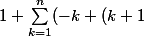)=n+1)
(1)
et
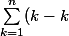=0)
(2)
on peut dire que ces deux sommes sont différentes quel que soit n, non?
Oui.
bombastus a écrit:Si on prends les limites on a :
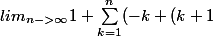))
)
pourquoi pourrait-t-on alors écrire une égalité entre ces 2 limites comme tu l'as fait avec des pointillés?
parce qu'elles sont des sommations par paquets d'une même série :

... , ou encore si on préfère
^k E( (k/2 +1))
comme l'a signalé Imod.
bombastus a écrit:Ce qui me dérange aussi, c'est que vous faîtes des associations de parenthèses sans penser au problème posé :
1 = 1
1 = (-1) + 2
1 = (-2) + 3
1 = (-3) + 4
1 = (-4) + 5
...
puis on fait la somme
si on arrête le raisonnement au rang n, on se retrouve toujours avec l'expression (1), jamais avec la (2). La somme de la suite d'Imod n'est pas non plus la même que celle qui est définit dans l'énoncé, alors pourquoi les étudier?
si si, on voit la (2) au dernier moment :
math_nour a écrit:En ajoutant membre à membre toutes ces inégalités, nous obtenons :
1 + 1 + 1 + 1 + 1 + 1 + ... = 1 + (-1) + 2 + (-2) + 3 + (-3) + 4 + (-4) + 5 + ...
Dans l'expression de droite, tous les termes s'éliminent deux à deux, soit :
1 + 1 + 1 + 1 + 1 + 1 + ... = 0
ici, à droite, l'auteur suggère le regroupement (1 -1) + (2-2) + ... quand il dit que les termes s'éliminent deux à deux.
