Droite d'intersection
22 messages
- Page 1 sur 2 - 1, 2
droite d'intersection
Etant donné les plans r1: 2x+5y-7z+2=0
r2: x+y-z+3=0
est-ce que l'angle diedre entre ces deux plans serait bien de 23,76 degre
et l'equation de la droite d'intersection de ces deux plans
est ce qu on peut dire que
x+y=-3 2x+5y= -2
x=-3-y 2(-3-y)+5y=-2
x=-13/3 -6-2y+5y=-2
-6+3y=-2
3y=-2+6
y= 4/3
Donc D:(x,y,z)=(-13/3,4/3,0)+t(1,1,-1) est-ce que c'est bien ceci??
Merci !!! :)
r2: x+y-z+3=0
est-ce que l'angle diedre entre ces deux plans serait bien de 23,76 degre
et l'equation de la droite d'intersection de ces deux plans
est ce qu on peut dire que
x+y=-3 2x+5y= -2
x=-3-y 2(-3-y)+5y=-2
x=-13/3 -6-2y+5y=-2
-6+3y=-2
3y=-2+6
y= 4/3
Donc D:(x,y,z)=(-13/3,4/3,0)+t(1,1,-1) est-ce que c'est bien ceci??
Merci !!! :)
1) Oui l'angle est bien 23.7646 °
2) Dans ton produit vectoriel il y a une erreur de signe
(on doit trouver (2,-5,-3))
3) à quoi correspond la direction de ce produit vectoriel ?
4) Pour déterminer la droite d'intersection des deux plans, tu peux aussi résoudre le système:
2x+5y-7z+2=0
x+y-z+3=0
en calculant x et y en fonction de z
Puis tu pourras poser z=t si tu veux une représentation paramétrique de ta droite d'intersection
2) Dans ton produit vectoriel il y a une erreur de signe
(on doit trouver (2,-5,-3))
3) à quoi correspond la direction de ce produit vectoriel ?
4) Pour déterminer la droite d'intersection des deux plans, tu peux aussi résoudre le système:
2x+5y-7z+2=0
x+y-z+3=0
en calculant x et y en fonction de z
Puis tu pourras poser z=t si tu veux une représentation paramétrique de ta droite d'intersection
Trouver les équations cartésiennes et résoudre un système.
1°) Déterminer l'équation cartésienne  du plan
du plan  .
.
Rappel : le plan est l'ensemble des points
est l'ensemble des points  tels que
tels que  ,
,  .
.
2°) En déduire un vecteur normal du plan
du plan  .
.
3°) passe par
passe par  et de vecteur normal
et de vecteur normal  .
.
4°) Déterminer un point de la droite
de la droite  et un vecteur directeur
et un vecteur directeur  de
de  , autrement dit déterminer un système d'équations paramétriques de
, autrement dit déterminer un système d'équations paramétriques de  .
.
5°) On s'assure que pour vérifier que
pour vérifier que  et donc dans notre cas
et donc dans notre cas  . Les coordonnées de
. Les coordonnées de  sont données par le triplet
sont données par le triplet  solution du système
solution du système  :
:
 ,
,  .
.
A toi de jouer.:king2:
 du plan
du plan  .
.Rappel : le plan
 est l'ensemble des points
est l'ensemble des points  tels que
tels que  ,
,  .
.2°) En déduire un vecteur normal
 du plan
du plan  .
.3°)
 passe par
passe par  et de vecteur normal
et de vecteur normal  .
.4°) Déterminer un point
 de la droite
de la droite  et un vecteur directeur
et un vecteur directeur  de
de  .
.5°) On s'assure que
 pour vérifier que
pour vérifier que  et donc dans notre cas
et donc dans notre cas  . Les coordonnées de
. Les coordonnées de  sont données par le triplet
sont données par le triplet  solution du système
solution du système  :
: ,
,  .
.A toi de jouer.:king2:
Trouver les équations cartésiennes et résoudre un système.
1°) Déterminer l'équation cartésienne 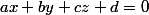 du plan
du plan ) .
.
Rappel : le plan) est l'ensemble des points
est l'ensemble des points ) tels que
tels que 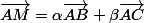 ,
, \in\mathbb{R}^2) .
.
2°) En déduire un vecteur normal) du plan
du plan ) .
.
3°)) passe par
passe par ) et de vecteur normal
et de vecteur normal ) .
.
4°) Déterminer un point) de la droite
de la droite  et un vecteur directeur
et un vecteur directeur ) de
de  , autrement dit déterminer un système d'équations paramétriques de
, autrement dit déterminer un système d'équations paramétriques de  .
.
5°) On s'assure que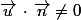 pour vérifier que
pour vérifier que \cap{D}\not=\empty) et donc dans notre cas
et donc dans notre cas \cap{D}=I) . Les coordonnées de
. Les coordonnées de  sont données par le triplet
sont données par le triplet ) solution du système
solution du système ) :
:
\left\{\begin{matrix}x=x_0+a^{'}t\\y=y_0+b^{'}t\\z=z_0+c^{'}t\\ax+by+cz+d=0\end{matrix}\right) ,
, 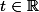 .
.
A toi de jouer.:king2:
Rappel : le plan
2°) En déduire un vecteur normal
3°)
4°) Déterminer un point
5°) On s'assure que
A toi de jouer.:king2:
Tu cherche l'équation sous la forme ax+by+cz = d
En quel classe es-tu ?
Façon simple de traiter le problème est de le mettre sous la forme d'une
équation matricielle :
1 0 -7 a d
-2 -1 0 * b = d
0 0 -3 c d
M * (a,b,c)' = (d,d,d)'
Tu as 3 équations avec 4 inconnus, donc tu peux choisir une de tes inconnues :
par exemple d = 3 (au début j'avais choisis d=1, mais ça donne des rationnels
pour a,b, et c ensuite)
Alors, tu obtiens (a,b,c)' = M^(-1)*(3,3,3)' avec M^(-1) la matrice
inverse de M
-4x+5y-z = 3 est donc une équation cartésienne de ton plan
En quel classe es-tu ?
Façon simple de traiter le problème est de le mettre sous la forme d'une
équation matricielle :
1 0 -7 a d
-2 -1 0 * b = d
0 0 -3 c d
M * (a,b,c)' = (d,d,d)'
Tu as 3 équations avec 4 inconnus, donc tu peux choisir une de tes inconnues :
par exemple d = 3 (au début j'avais choisis d=1, mais ça donne des rationnels
pour a,b, et c ensuite)
Alors, tu obtiens (a,b,c)' = M^(-1)*(3,3,3)' avec M^(-1) la matrice
inverse de M
-4x+5y-z = 3 est donc une équation cartésienne de ton plan
Sam Mar a écrit:Tu cherche l'équation sous la forme ax+by+cz = d
En quel classe es-tu ?
Façon simple de traiter le problème est de le mettre sous la forme d'une
équation matricielle :
1 0 -7 a d
-2 -1 0 * b = d
0 0 -3 c d
M * (a,b,c)' = (d,d,d)'
Tu as 3 équations avec 4 inconnus, donc tu peux choisir une de tes inconnues :
par exemple d = 3 (au début j'avais choisis d=1, mais ça donne des rationnels
pour a,b, et c ensuite)
Alors, tu obtiens (a,b,c)' = M^(-1)*(3,3,3)' avec M^(-1) la matrice
inverse de M
-4x+5y-z = 3 est donc une équation cartésienne de ton plan
Voir mon précédent rappel au réglement. Il n'y en aura pas d'autre....
Merci beaucoup les gars ,:) Par contre c'etait pas la reponse a ma question donc y ma pas vraiment donner la reponse !!!.....Il faut que je trouve le point d intersection de ce plan avec la droite d'equation x-7/12=y+1/-6=z-2/-2
donc comment je peux trouver un point d intersection avec -4x+5y-z=3 faut je trouve cest quoi x,y,z??? Merci!!
donc comment je peux trouver un point d intersection avec -4x+5y-z=3 faut je trouve cest quoi x,y,z??? Merci!!
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
