Devoir de vacance diifiiciile !!!
22 messages
- Page 1 sur 2 - 1, 2
devoir de vacance diifiiciile !!!
Bonjour,
Ce devoir est à rendre pour dans une semaine mais je n'y arrive pas jespère donc que vous pourrez m'aider...
Merci d'avance pour vos reponses.
Il s'agit tout d'abord d'un système d'équation:
x/2 - y/3 = 1
3x - 5y = -3
Merci...
Puis de ce système:
Dans une salle, il y a 3 fois plus de garçons que de filles ; 6 garçons quittent la salle et 4 filles arrivent il y a alors autant de garçons que de filles.
Combien y avait-il de garçons et de filles au départ dans la salle ?
Merci pour vos reponces ...
Ce devoir est à rendre pour dans une semaine mais je n'y arrive pas jespère donc que vous pourrez m'aider...
Merci d'avance pour vos reponses.
Il s'agit tout d'abord d'un système d'équation:
x/2 - y/3 = 1
3x - 5y = -3
Merci...
Puis de ce système:
Dans une salle, il y a 3 fois plus de garçons que de filles ; 6 garçons quittent la salle et 4 filles arrivent il y a alors autant de garçons que de filles.
Combien y avait-il de garçons et de filles au départ dans la salle ?
Merci pour vos reponces ...
re
x/2 - y/3 = 1
3x - 5y = -3
Multiplie la première par (-6) et additionne tes deux équations
ou alors multiplie la première par 2 est trouve une équation du type x = ...y + ... et insère x dans la seconde équation et tu arrive à résoudre y
Pour le deuxième système, pose x le nombre de garçons, y le nombre de filles, pose les deux équations et résoud les de la même manière que pour ton premier système
3x - 5y = -3
Multiplie la première par (-6) et additionne tes deux équations
ou alors multiplie la première par 2 est trouve une équation du type x = ...y + ... et insère x dans la seconde équation et tu arrive à résoudre y
Pour le deuxième système, pose x le nombre de garçons, y le nombre de filles, pose les deux équations et résoud les de la même manière que pour ton premier système
re
tu peux poster tes réponses si tu veux qu'on les vérifie !! (mais si tu le fais, mets un peu ton détail,qu'on puisse corriger le cas échéant)
bonjour j aimerais que vous maidiez pour se probleme svp
soit f,g et h les fonction affines definies par f:x->-2x+5 ; g:x->2x+5 ; h:x->2/3x+8/3
les representations grafique de f g et h definnisent un triangle ABC(xa
2.calculer les coordonnees des point A,Bet C
3.a-- resoudre par calcum l iequation : -2x+5
voila merci
soit f,g et h les fonction affines definies par f:x->-2x+5 ; g:x->2x+5 ; h:x->2/3x+8/3
les representations grafique de f g et h definnisent un triangle ABC(xa
2.calculer les coordonnees des point A,Bet C
3.a-- resoudre par calcum l iequation : -2x+5
voila merci
bonjour,
sais-tu qu'il y a deux façons de résoudre un système à 2 équations : par substitution et par combinaison.
Par combinaison : il faut éliminer une des inconnues en additionnant ou en soustrayant les 2 équations
x/2 - y/3 = 1 (1)
{
3x - 5y = -3 (2)
ici si tu multiplies (1) par 6, tu obtiens un système équivalent :
(1)*6---> 6x/2-6y/3=1*6 soit 3x-2y=6
tu as le système suivant :
3x-2y=6
{
3x-5y=-3
(1)-(2)=(3x-2y)-(3x-5y)=6-(-3)
-2y+5y=6+3=9
3y=9
y=9/3=3
on remplace y par sa valeur dans (1) ou (2) pour trouver x
3x-5y=-3
3x-5*3=-3
3x=15-3=12
x=12/3=4
vérification :
3x-2y=3*4-2*3=12-6=6
3x-5y=3*4-5*3=12-15=-3
par substitution : on exprime une des inconnues en fonction de l'autre d'après une des équations et on remplace dans l'autre
(1) x/2-y/3=1---->3x/6=6/6+2y/6
3x=6+2y
x=6/3+2y/3=2+2y/3
(2) 3x-5y=-3
3(2+2y/3)-5y=-3
6+6y/3-5y=-3
2y-5y=-3-6
-3y=-9
y=-9/-3=3
x=2+2y/3=2+2*3/3=2+2=4
S={4;3}
sais-tu qu'il y a deux façons de résoudre un système à 2 équations : par substitution et par combinaison.
Par combinaison : il faut éliminer une des inconnues en additionnant ou en soustrayant les 2 équations
x/2 - y/3 = 1 (1)
{
3x - 5y = -3 (2)
ici si tu multiplies (1) par 6, tu obtiens un système équivalent :
(1)*6---> 6x/2-6y/3=1*6 soit 3x-2y=6
tu as le système suivant :
3x-2y=6
{
3x-5y=-3
(1)-(2)=(3x-2y)-(3x-5y)=6-(-3)
-2y+5y=6+3=9
3y=9
y=9/3=3
on remplace y par sa valeur dans (1) ou (2) pour trouver x
3x-5y=-3
3x-5*3=-3
3x=15-3=12
x=12/3=4
vérification :
3x-2y=3*4-2*3=12-6=6
3x-5y=3*4-5*3=12-15=-3
par substitution : on exprime une des inconnues en fonction de l'autre d'après une des équations et on remplace dans l'autre
(1) x/2-y/3=1---->3x/6=6/6+2y/6
3x=6+2y
x=6/3+2y/3=2+2y/3
(2) 3x-5y=-3
3(2+2y/3)-5y=-3
6+6y/3-5y=-3
2y-5y=-3-6
-3y=-9
y=-9/-3=3
x=2+2y/3=2+2*3/3=2+2=4
S={4;3}
Oui je suis d'accord ! Ta soeur profite de ses vacances à la plage avec ses copains, copines et toi tu es mandaté par elle pour résoudre son problème, c'est quoi cette arnaque ?:hum:
Et moi qui suis en train de te taper un cours avec la méthode et ton exo résolu comme exemple...:--:
Et moi qui suis en train de te taper un cours avec la méthode et ton exo résolu comme exemple...:--:
yvelines78 a écrit:ne crois-tu pas que tu nous dois des éclaircissements!!!
Tu anticipes drôlement... En effet les systèmes linéaires sont au programme de 3ème.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues et
et  . Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques
. Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques 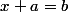 ;
; 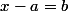 ;
; 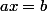 ;
; 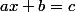 .
.
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
:\left\{\begin{matrix} \frac{1}{2} x-\frac{1}{3} y=1,\ & \mbox{(L_1) } \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
Choisissons ici d'éliminer le de la 1ère équation
de la 1ère équation  . On multiplie
. On multiplie  et/ou
et/ou 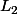 par des coefficients judiscieusement choisi pour que le coefficient de
par des coefficients judiscieusement choisi pour que le coefficient de  de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de dans
dans  , puis on remplacera (on substitue) cette valeur dans
, puis on remplacera (on substitue) cette valeur dans 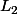 pour trouver
pour trouver  .
.
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
} \\ 3x-5y=-3,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
} \\ 3x-5\times 3=-3,\ & \mbox{(L_2) } \end{matrix}\right)
On a remplacé la valeur trouvé de dans la 2ème équation.
dans la 2ème équation.
} \\ 3x=-3+15=12,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{x=4},\ & \mbox{(L_2)} \end{matrix}\right)
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
2)
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
L'énoncé revient à résoudre le système suivant :
:\left\{\begin{matrix} x=3y,\ & \mbox{(L_1)} \\ x-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
En substituant l'expression de de
de  dans
dans 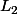 il vient :
il vient :
} \\ 3y-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 2y=10,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{y=5},\ & \mbox{(L_2)} \end{matrix}\right)
Ici on a d'abord trouvé dans
dans 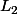 puis on a remplacé sa valeur dans
puis on a remplacé sa valeur dans  pour trouver
pour trouver  .
.
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
Choisissons ici d'éliminer le
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
On a remplacé la valeur trouvé de
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
2)
Soit
Soit
L'énoncé revient à résoudre le système suivant :
En substituant l'expression de
Ici on a d'abord trouvé
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Tu anticipes drôlement... En effet les systèmes linéaires sont au programme de 3ème.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues et
et  . Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques
. Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques 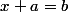 ;
; 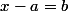 ;
; 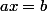 ;
; 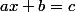 .
.
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
:\left\{\begin{matrix} \frac{1}{2} x-\frac{1}{3} y=1,\ & \mbox{(L_1) } \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
Choisissons ici d'éliminer le de la 1ère équation
de la 1ère équation  . On multiplie
. On multiplie  et/ou
et/ou 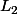 par des coefficients judiscieusement choisi pour que le coefficient de
par des coefficients judiscieusement choisi pour que le coefficient de  de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de dans
dans  , puis on remplacera (on substitue) cette valeur dans
, puis on remplacera (on substitue) cette valeur dans 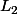 pour trouver
pour trouver  .
.
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
} \\ 3x-5y=-3,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
} \\ 3x-5\times 3=-3,\ & \mbox{(L_2) } \end{matrix}\right)
On a remplacé la valeur trouvé de dans la 2ème équation.
dans la 2ème équation.
} \\ 3x=-3+15=12,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{x=4},\ & \mbox{(L_2)} \end{matrix}\right)
La solution du système est le couple=(4;3))
2)
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
L'énoncé revient à résoudre le système suivant :
:\left\{\begin{matrix} x=3y,\ & \mbox{(L_1)} \\ x-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
En substituant l'expression de de
de  dans
dans 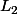 il vient :
il vient :
} \\ 3y-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 2y=10,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{y=5},\ & \mbox{(L_2)} \end{matrix}\right)
Ici on a d'abord trouvé dans
dans 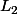 puis on a remplacé sa valeur dans
puis on a remplacé sa valeur dans  pour trouver
pour trouver  .
.
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
Choisissons ici d'éliminer le
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
On a remplacé la valeur trouvé de
La solution du système est le couple
2)
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
Soit
Soit
L'énoncé revient à résoudre le système suivant :
En substituant l'expression de
Ici on a d'abord trouvé
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Tu anticipes drôlement... En effet les systèmes linéaires sont au programme de 3ème.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues et
et  . Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques
. Or résoudre une équation à 2 inconnues tu ne sais pas faire. En 5ème tu vois tout juste les équations basiques 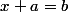 ;
; 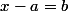 ;
; 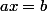 ;
; 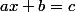 .
.
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
:\left\{\begin{matrix} \frac{1}{2} x-\frac{1}{3} y=1,\ & \mbox{(L_1) } \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
Choisissons ici d'éliminer le de la 1ère équation
de la 1ère équation  . On multiplie
. On multiplie  et/ou
et/ou 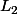 par des coefficients judiscieusement choisi pour que le coefficient de
par des coefficients judiscieusement choisi pour que le coefficient de  de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
de la 1ère et 2ème équation soit opposés, ils disparaitront donc par addition.
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de dans
dans  , puis on remplacera (on substitue) cette valeur dans
, puis on remplacera (on substitue) cette valeur dans 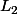 pour trouver
pour trouver  .
.
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
} \\ 3x-5y=-3,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 3x-5y=-3,\ & \mbox{(L_2) } \end{matrix}\right)
} \\ 3x-5\times 3=-3,\ & \mbox{(L_2) } \end{matrix}\right)
On a remplacé la valeur trouvé de dans la 2ème équation.
dans la 2ème équation.
} \\ 3x=-3+15=12,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{x=4},\ & \mbox{(L_2)} \end{matrix}\right)
La solution du système est le couple=(4;3))
2)
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
Soit le nombre de garçons au départ dans la classe,
le nombre de garçons au départ dans la classe,  doit être un entier positif (entier naturel)
doit être un entier positif (entier naturel)
L'énoncé revient à résoudre le système suivant :
:\left\{\begin{matrix} x=3y,\ & \mbox{(L_1)} \\ x-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
En substituant l'expression de de
de  dans
dans 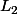 il vient :
il vient :
} \\ 3y-6=y+4,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ 2y=10,\ & \mbox{(L_2)} \end{matrix}\right)
} \\ \b{y=5},\ & \mbox{(L_2)} \end{matrix}\right)
Ici on a d'abord trouvé dans
dans 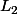 puis on a remplacé sa valeur dans
puis on a remplacé sa valeur dans  pour trouver
pour trouver  .
.
La solution du système est le couple=(15;5))
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Il y a 2 méthodes pour les résoudre (substitution et addition/combinaison linéaire - Pivot de Gauss) et 1 méthode graphique basée sur la représentation graphique de fonctions affines permettant de donner une approximation de la solution du système par lecture graphique.
Il est difficile de te faire un cours complet dans un forum. Surtout que tu es bien jeune et il va t'être difficile de comprendre et assimiler la résolution des systèmes linéaires.
Enfin, ton système présente 2 équations à 2 inconnues
Donc il te faut transformer les équations en équations à une inconnue.
Tu as 2 questions pour ton problème, basé sur les systèmes :
Je vais te montrer comment faire. Considère que c'est exercice résolu pour te montrer l'exemple.
Mais franchement tu ferais mieux d'aller à la plage ou la piscine, t'éclater avec tes copains, copines ou anticiper sur la 4ème mais pas sur la 3ème.
Bref, allons y :
Le principe de la méthode combinaison est d'éliminer une inconnue d'une équation par addition (il est toujours plus simple d'additionner que de soustraire...).
Voici ton système :
1)
Choisissons ici d'éliminer le
La 2ème équation va rester en attente jusqu'à ce que l'on trouve la valeur de
Il faut savoir aussi qu'on a le droit de multiplier les 2 membres d'une égalité par un même nombre sans en changer les solutions. On la le droit d'ajouter ou de soustraire membre à membre les 2 équations.
Les systèmes écrits les uns sous les autres sont équivalents. On obtient :
On a remplacé la valeur trouvé de
La solution du système est le couple
2)
La 2ème question de ton problème n'a évidemment rien à voir avec la 1ère mais il s'agit ici de modéliser le problème par un système. C'est à toi de le trouver ce système, on ne te le donne pas.
Il faut tout d'abord définir les inconnues ; puis les éventuelles contraintes sur chaque inconnues ; traduire l'énoncé avec un système ; résoudre le système ; vérifier qu'on obéit bien aux contraintes ; formuler une réponse concrète au problème.
Soit
Soit
L'énoncé revient à résoudre le système suivant :
En substituant l'expression de
Ici on a d'abord trouvé
La solution du système est le couple
Ainsi il y avait 15 garçons et 5 filles dans la classe. Ces 2 valeurs sont bien des entiers naturels et vérifient bien les conditions de l'énoncé.
Non, système linéaire veut dire système d'équations linéaires (à 2 inconnues en 3ème et plus en 2nde, 1ère...) de la forme 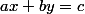 par opposition aux systèmes non linéaires du type
par opposition aux systèmes non linéaires du type  par exemple. Les systèmes qu'on étudient en 3ème sont exactement les même que ceux de 2nde et on utilise d'ailleurs les mêmes méthodes pour les résoudre. Ce sont les systèmes linéaires à 2 inconnues. Au delà de la seconde on apprend le pivot de Gauss et les changements de variables pour résoudre les systèmes à plus de 2 inconnues et aux équations non linéaires.
par exemple. Les systèmes qu'on étudient en 3ème sont exactement les même que ceux de 2nde et on utilise d'ailleurs les mêmes méthodes pour les résoudre. Ce sont les systèmes linéaires à 2 inconnues. Au delà de la seconde on apprend le pivot de Gauss et les changements de variables pour résoudre les systèmes à plus de 2 inconnues et aux équations non linéaires.
Je crois que c'est confus dans ton esprit ou alors Il faudra que tu m'expliques la différence entre "les systèmes d'équations (et d'inéquations) à deux inconnues qu'on voit en troisième" et "les systèmes linéaires de 2nde"...
@+:++:
Je crois que c'est confus dans ton esprit ou alors Il faudra que tu m'expliques la différence entre "les systèmes d'équations (et d'inéquations) à deux inconnues qu'on voit en troisième" et "les systèmes linéaires de 2nde"...
@+:++:
Timothé Lefebvre a écrit:Juste une précision par rapport aux systèmes linéaires, on les voit en seconde ; ce sont les systèmes d'équations (et d'inéquations) à deux inconnues qu'on voit en troisième (on les résoud par combinaison et substitution d'ailleurs).
Fanatic a écrit:Non, système linéaire veut dire système d'équations linéaires (à 2 inconnues en 3ème et plus en 2nde, 1ère...) de la formepar opposition aux systèmes non linéaires du type
par exemple. Les systèmes qu'on étudient en 3ème sont exactement les même que ceux de 2nde et on utilise d'ailleurs les mêmes méthodes pour les résoudre. Ce sont les systèmes linéaires à 2 inconnues. Au delà de la seconde on apprend le pivot de Gauss et les changements de variables pour résoudre les systèmes à plus de 2 inconnues et aux équations non linéaires.
Je crois que c'est confus dans ton esprit ou alors Il faudra que tu m'expliques la différence entre "les systèmes d'équations (et d'inéquations) à deux inconnues qu'on voit en troisième" et "les systèmes linéaires de 2nde"...
@+:++:
On voit quand même la différence de présentation entre le message de Yvelines78 et Fanatic. Bravo Fanatic pour tes efforts de présentation en
Fanatic a écrit:Non, système linéaire veut dire système d'équations linéaires (à 2 inconnues en 3ème et plus en 2nde, 1ère...) de la formepar opposition aux systèmes non linéaires du type
par exemple. Les systèmes qu'on étudient en 3ème sont exactement les même que ceux de 2nde et on utilise d'ailleurs les mêmes méthodes pour les résoudre. Ce sont les systèmes linéaires à 2 inconnues. Au delà de la seconde on apprend le pivot de Gauss et les changements de variables pour résoudre les systèmes à plus de 2 inconnues et aux équations non linéaires.
Je crois que c'est confus dans ton esprit ou alors Il faudra que tu m'expliques la différence entre "les systèmes d'équations (et d'inéquations) à deux inconnues qu'on voit en troisième" et "les systèmes linéaires de 2nde"...
@+:++:
Je crois plutôt que je me suis mal exprimé, pardonne-moi ... Je connais bien le programme de troisième et aussi celui de seconde et je peux affirmer sans me tromper que la dénomination "système linéaire" n'est pas étudiée en troisième ; après va savoir pourquoi !
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

