Relation loi binomiale et loi gamma
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
NELLLY
- Membre Naturel
- Messages: 29
- Enregistré le: 09 Mar 2008, 22:03
-
 par NELLLY » 13 Juil 2008, 17:36
par NELLLY » 13 Juil 2008, 17:36
Salut
comment on peut établir la relation suivante:
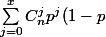^{n_j}=\frac{\rm \Gamma(n+1)}{\rm \Gamma(n-x)\Gamma(x+1)} \int_0^{1-p} w^{n-x-1} (1-w)^x dw)
avec
=(n-1)!)
Votre aide sera trés précieuse. :id:
-
john32
- Membre Relatif
- Messages: 239
- Enregistré le: 08 Juil 2008, 10:34
-
 par john32 » 15 Juil 2008, 07:42
par john32 » 15 Juil 2008, 07:42
Est tu sure de la puissance de (1-p) car nj me paraît étrange e^t peu compréhensible vis à vis du pb.
-
NELLLY
- Membre Naturel
- Messages: 29
- Enregistré le: 09 Mar 2008, 22:03
-
 par NELLLY » 20 Juil 2008, 15:07
par NELLLY » 20 Juil 2008, 15:07
Salut
je me suis trompé c'est
^{(n-j)})
, le premier terme c'est la fonction de répartition de la loi binomiale au point x.
-
kaya
- Membre Naturel
- Messages: 91
- Enregistré le: 03 Aoû 2005, 15:33
-
 par kaya » 20 Juil 2008, 15:36
par kaya » 20 Juil 2008, 15:36
je n'est pas encore essayé mais d'ici je peut déjà voir une similarité entre les 2 termes mais je pense que cette équation ne soit valable que pour n très grand je crois; ensuite tu fais Riemann...c'est juste une intuition. pas nécessairement juste.
T'as déjà essayé?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités