Récurrence

par **baptisted** » 19 Juil 2008, 20:09

Bonsoir,

Je voudrais savoir si on a le droit de faire une récurrence sur les entiers pairs uniquement.

Par exemple : On considère la proposition P(n)

On montre que P(0) vraie.
On montre que P(n) vraie implique P(n+2) vraie
, ?????.

Est-bien rigoureux ? Merci de vos réponses.

par **Clembou** » 19 Juil 2008, 20:56

baptisted a écrit:Bonsoir,

Je voudrais savoir si on a le droit de faire une récurrence sur les entiers pairs uniquement.

Par exemple : On considère la proposition P(n)

On montre que P(0) vraie.
On montre que P(n) vraie implique P(n+2) vraie
, ?????.
Est-bien rigoureux ? Merci de vos réponses.

Ce n'est pas ce que dit le principe de réccurence. Parce que tu as vérifie la proposition à l'ordre

, tu veux la démontrer à l'ordre

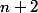
mais si la propriété n'est pas vraie à l'ordre

...

par **baptisted** » 19 Juil 2008, 21:00

Pourtant si on a P(0) vraie et P(n)=>P(n+2), on a :
[center]P(0)=>P(2)=>P(4) ect...
[left]Je ne comprends pas pourquoi cela ne marche pas

[/left]
[/center]

par **Clembou** » 19 Juil 2008, 21:01

baptisted a écrit:Pourtant si on a P(0) vraie et P(n)=>P(n+2), on a :
[center]P(0)=>P(2)=>P(4) ect...
[left]Je ne comprends pas pourquoi cela ne marche pas

[/left]
[/center]

oui et

???

????

EDIT : Ah non, tu me dis que

,

doit être verifié. Alors là je ne sais pas !

par **baptisted** » 19 Juil 2008, 21:02

Mais si P(2n+1) ne nous intéresse pas ?

par **Clembou** » 19 Juil 2008, 21:04

baptisted a écrit:Mais si P(2n+1) ne nous intéresse pas ?

Ok ! J'avais pas vu... Alors là ce n'est pas très commun ! Pourquoi tu veux faire ça ? Tu veux juste savoir ou tu as un exercice sur ça ?

par **baptisted** » 19 Juil 2008, 21:06

En fait j'essayais de voir plusieurs manières de montrer que si p² est pair alors p l'est aussi... et donc je me demandais si on pouvait faire une récurrence uniquement sur les entiers pairs.

EDIT : Mais bon si cette idée de récurrence sur 2

est complètement tordue, j'abandonne...

Juste, juste, peut-on dire que si on travail sur l'ensemble {2;4;6;...;2k...} on a :

le rang 0 pour n = 0
le rang 1 pour n = 2
le rang 3 pour n = 4
... ??

La récurrence est-elle seulement sur

ou sur tout ensemble dont les éléments appartiennent à

??

par **Clembou** » 19 Juil 2008, 21:12

baptisted a écrit:En fait j'essayais de voir plusieurs manières de montrer que si p² est pair alors p l'est aussi... et donc je me demandais si on pouvait faire une récurrence uniquement sur les entiers pairs.

Dans ce genre de demonstration, ce n'est pas très rigoureux d'utiliser le principe de réccurence car ce principe s'applique sur tous les entiers.

Par exemple, si tu veux démontrer ceci :

pair alors

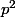
pair
tu peux remplacer

par

et tu démontres cette propriété pour tout

. Là oui ! Tu appliques le principe de reccurence. Dans l'autre sens, je ne pense pas que ça soit le "vrai" principe de reccurence.

par **baptisted** » 19 Juil 2008, 21:16

Clembou a écrit:Dans ce genre de démonstration, ce n'est pas très rigoureux d'utiliser le principe de récurrence car ce principe s'applique sur tous les entiers.

Ok donc pas d'éléments choisis de

... et forcément {

}
Merci beaucoup pour tes réponses :we: !

par **Clembou** » 19 Juil 2008, 21:20

baptisted a écrit:Ok donc pas d'éléments choisis de ... et forcément { }
Merci beaucoup pour tes réponses :we: !

Oui voilà... Enfin, c'est ce que j'ai appris dans mes études et c'est ce qui est marqué sur tous les sites de mathématiques :

http://fr.wikipedia.org/wiki/Raisonnement_par_r%C3%A9currence (par exemple :++:)

Il y a d'autres formes de réccurence... Regarde la page que je t'ai donné...

par **baptisted** » 19 Juil 2008, 21:31

Wikipédia a écrit: Généralisations

Le raisonnement par récurrence se généralise naturellement, sous la forme de la récurrence bien fondée indiquée ci-dessus, aux ensembles sur lesquels on peut définir un bon ordre (1), voir nombre ordinal et récurrence transfinie, ou simplement une relation bien fondée.

On peut le généraliser pour démontrer non plus des propriétés universelles sur les entiers naturels, mais par exemple sur les suites d'entiers ou sur les fonctions des entiers vers les entiers.

(1) : Je crois que 2

répond bien à cette condition :

baptisted a écrit:Juste, juste, peut-on dire que si on travail sur l'ensemble {2;4;6;...;2k...} on a :

le rang 0 pour n = 0
le rang 1 pour n = 2
le rang 3 pour n = 4
...

Il faut juste remplacer "rang" par "ordre"... Mais je crois que c'est un peu la même chose ici, non ?

par **Clembou** » 19 Juil 2008, 21:34

baptisted a écrit:(1) : Je crois que 2 répond bien à cette condition :

Il faut juste remplacer "rang" par "ordre"... Mais je crois que c'est un peu la même chose ici, non ?

Ok ok ! Donc oui, tu peux ! :++:

par **Zweig** » 19 Juil 2008, 21:59

Baptised > Montrer que

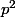
pair ->

pair, vaut mieux faire ça par congruence.

Un carré pair est toujours congru à 0 mod 4. On vérifit aisément que seules les congruences

vérifient

, c'est-à-dire lorsque

est pair.

par **baptisted** » 19 Juil 2008, 22:04

Zweig a écrit:Un carré pair est toujours congru à 0 mod 4.

Je n'avais pas remarqué :mur: (et pourtant j'aurais dû...)
C'est vrai que ça simplifie les choses...

par **Zweig** » 19 Juil 2008, 22:05

Lorsque qu'un carré est impair, il est congru à 1 mod 4 :happy2:

par **baptisted** » 20 Juil 2008, 10:46

Donc si je veux démonter p pair p² pair, cela me donne :

=>

On suppose qu'il existe

tel que p = 2k
On a alors p² = 4k² soit p² = 2k' avec k'= 2k².

<=

On suppose qu'il existe

tel que p² = 2k
Dès lors,

Récurrence

Récurrence

Qui est en ligne