Fonction injective

par **Clise** » 17 Juil 2008, 10:52

Bonjour,

J'ai un doute ... Est ce que une fonction injective d'un ensemble vers ce même ensemble est bijective ?

J'ai un peu honte de poser une question comme ça, mais je n'ai pas trouvé ma réponse quelque part.

Merci pour vos réponses

par **nonam** » 17 Juil 2008, 10:59

Si l'ensemble est fini : oui.
S'il ne l'est pas,ce n'est pas nécessaire : tu devrais trouver des tas de contre-exemples sur R...

par **Clise** » 17 Juil 2008, 11:07

en l'occurence mon ensemble peut être finie ou non ...
donc c'est pas vraie :S
Merci pour ta réponse

par **barbu23** » 17 Juil 2008, 11:24

Salut :
Comme l'a dit "nonam" , si l'ensemble est fini, oui, il y'a bijection par cardinalité :
Soit :

un ensemble fini, telle que :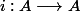

est injective ...
Il suffit de monter que

est surjective :
Pusique :

est une application, alors, toute element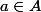

a une unique image

dans

par

et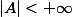

... Par conséquent :

Donc, surjective !

par **barbu23** » 17 Juil 2008, 11:30

Si

n'est pas fini ( par ex.

)
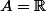Tu imagines dans ta tête un graphe definie sur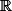

et à valeurs dans

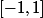et qui reprensente une fonction

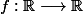croissante par exemple, alors, il n'est pas surjective ( car

) ... donc, n'est pas bijective ... !
Bref, toute application injective, non surjective et non bijective ... !
Cordialement ... !

par **Clise** » 17 Juil 2008, 12:06

Merci, j'ai tout compris :zen:

Fonction injective

fonction injective

Qui est en ligne