On donne
Je dois trouver toutes les fonctions f.
Quelle est la méthode à employer ? (je suppose qu'il va falloir que j'intègre par rapport à x pour la 1ère égalité, puis par rapport à y pour la 2ème non ..?)
Merci pour vos indications.
Dérivées partielles
8 messages
- Page 1 sur 1
dérivées partielles
par MacManus » 11 Juil 2008, 18:42
Bonjour !
On donne = (a+2)x^{a+1}y^{-a}-y^3 x^2 \\ \frac{\partial f}{\partial y}(x,y) = -ax^{a+2}y^{-a-1}+3x^{-1}y^2)
, a étant un réel fixé, avec x>0 et y>0.
Je dois trouver toutes les fonctions f.
Quelle est la méthode à employer ? (je suppose qu'il va falloir que j'intègre par rapport à x pour la 1ère égalité, puis par rapport à y pour la 2ème non ..?)
Merci pour vos indications.
On donne
Je dois trouver toutes les fonctions f.
Quelle est la méthode à employer ? (je suppose qu'il va falloir que j'intègre par rapport à x pour la 1ère égalité, puis par rapport à y pour la 2ème non ..?)
Merci pour vos indications.
par nonam » 12 Juil 2008, 18:02
En intégrer une seule des 2 suffit :
tu intègres par exemple la première. La différence avec les dérivées partielles c'est que la constante d'intégration sera ici une fonction
, dépendant de y.
Tu dérives ensuite l'expression trouvée, par rapport à y.
Puis avec la seconde expression de
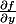
, tu pourra déterminer 
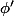
, puis , et tu auras f.
Mais es-tu sûr du système, car ne trouve pas de solution ici ?
tu intègres par exemple la première. La différence avec les dérivées partielles c'est que la constante d'intégration sera ici une fonction
Tu dérives ensuite l'expression trouvée, par rapport à y.
Puis avec la seconde expression de
Mais es-tu sûr du système, car ne trouve pas de solution ici ?
par Daniel-Jackson » 12 Juil 2008, 18:23
nonam a écrit:Mais es-tu sûr du système, car ne trouve pas de solution ici ?
Je pense aussi il y a un soucis, sans doute au niveau du dernier terme d'une des deux équations ( peut être la deuxième ?) .
Parce que la solution est clairement donnée en intégrant la première équation.
par nonam » 12 Juil 2008, 18:34
Il doit y avoir plusieurs façons de modifier ce système pour qu'il ait des solution.
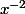
au lieu de 
à la fin de la première équation conviendrait.
par MacManus » 13 Juil 2008, 01:49
C'est noté ! merci nonam et Daniel-Jackson. Dès que j'ai quelque chose sous la dent, je le dirai.
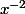
D'autre part vous avez raison, il s'agit bien de (à la fin de la 1ère équation)
merci
D'autre part vous avez raison, il s'agit bien de
merci
par MacManus » 14 Juil 2008, 07:52
Je reprends mon système de départ :
 = (a+2)x^{a+1}y^{-a}-y^3 x^{-2 }\\ \frac{\partial f}{\partial y}(x,y) = -ax^{a+2}y^{-a-1}+3x^{-1}y^2)
pour tout réel fixé a et pour x>0, y>0, j'obtiens :
 = x^{a+2}y^{-a}+x^{-1}y^3)
(En dérivant par rapport à x ou par rapport à y, je retombe bien sur une des dérivées partielles de mon système). Cependant, je ne parviens pas à expliciter et ...
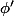
Merci encore
pour tout réel fixé a et pour x>0, y>0, j'obtiens :
(En dérivant par rapport à x ou par rapport à y, je retombe bien sur une des dérivées partielles de mon système). Cependant, je ne parviens pas à expliciter
Merci encore
par fatal_error » 14 Juil 2008, 08:38
Bonjour,
Je reprends ta solution f(x,y).
Pour la premiere equation on a :
 = x^{a+2}y^{-a}+x^{-1}y^3+\phi(y))
Pour la deuxieme
 = x^{a+2}y^{-a}+x^{-1}y^3+\phi'(x))
Comme tu l'as dit f(x,y) est solution des deux equations cad
 = x^{a+2}y^{-a}+x^{-1}y^3+\phi(y)\\<br />\phi(x)=\phi'(y))
Ici, tu peux exploiter le fait que si chaque fonction dépend d'une variable différente, alors il n'y a plus l'égalité.
Je reprends ta solution f(x,y).
Pour la premiere equation on a :
Pour la deuxieme
Comme tu l'as dit f(x,y) est solution des deux equations cad
Ici, tu peux exploiter le fait que si chaque fonction dépend d'une variable différente, alors il n'y a plus l'égalité.
la vie est une fête 
par nonam » 14 Juil 2008, 11:10
Sinon, qui revient au même :
Pour la première équation on a : = x^{a+2}y^{-a} +x^{-1}y^3 + \phi (y))
, puis en dérivant cette égalité par rapport à y :
 = -ax^{a+2}y^{-a-1} +3x^{-1}y^2 + \phi '(y))
Et avec l'autre expression de)
, on trouve 
.
Pour la première équation on a :
Et avec l'autre expression de
8 messages
- Page 1 sur 1
Qui est en ligne
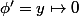
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :