calculer
Système trigo [pour se distraire]
9 messages
- Page 1 sur 1
mathelot a écrit:ça m'a l'air inexact. :hum:
Bah pourquoi ? tu peux remplacer et tu verras que ça colle très bien.
En fait, j'ai utilisé la formule sina+sinb et cosa+cosb
j'ai divisé, en supposant que cos((a-b)/2) était différent de 0, soit a-b différent de Pi (ce qui est le cas, sinon cosa+cosb=0), de manière à obtenir tan((a+b)/2) = quelque chose
j'en tire a+b.
Ensuite je mets au carré les deux équations
j'additionne
j'en tire que cos(a-b) = quelque chose
donc je déduis a-b.
Donc je déduis a et b.
PS : effectivement je n'ai pas parlé du modulo Pi pour tan et 2Pi pour cos.
solution
re,
en ajoutant la somme des carrés des deux égalités, on obtient:
=\frac{63}{65})
en factorisant les deux membres de gauches de chaque égalité
et en quotientant:
=\frac{7}{4})
avec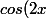=\frac{1-\tan^2(x)}{1+\tan^2(x)}) :
:
= - \frac{33}{65})
d'où
\cos(b)=\frac{1}{2} \left(\cos(a+b)+\cos(a-b) \right)=\frac{3}{13} \\<br />\cos(a)+\cos(b)=\frac{64}{65} \\)
) et
et ) sont solutions de:
sont solutions de:

d'où:
, \cos(b) \in \{ \frac{3}{5} ,\frac{5}{13} \})
On retrouve les triplets pythagoriciens dont je suis parti.
Il y a peut être moyen de rendre cet exo plus sexy, plus attrayant ? :zen:
et avec trois arcs a,b,c ?
en ajoutant la somme des carrés des deux égalités, on obtient:
en factorisant les deux membres de gauches de chaque égalité
et en quotientant:
avec
d'où
d'où:
On retrouve les triplets pythagoriciens dont je suis parti.
Il y a peut être moyen de rendre cet exo plus sexy, plus attrayant ? :zen:
et avec trois arcs a,b,c ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
