Convexité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 06 Juil 2008, 17:51
par MacManus » 06 Juil 2008, 17:51
Bonsoir à tous
Voila j'ai une petite question sur la convexité d'une fonction. Elle est définie pour tout (x,y,z)
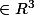
dans R par : f(x,y,z) = x²+xy+ay²+z²
A quelle(s) condition(s) sur le réel a f est-elle convexe?Je sais que dans R² par exemple, f est convexe ssi pour tout (x,y)

et tout

,
 y) \le \lambda f(x) + (1- \lambda) f(y))
.
Et pour

? quelle(s) méthode(s) suivre ? (dérivées partielles....)
On reconnait aussi en f l'expression d'une forme quadratique. Est-il préférable de suivre cette piste ?...
Merci beaucoup pour vos précisions!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Juil 2008, 18:25
par tize » 06 Juil 2008, 18:25
Bonjour,
je ne l'ai pas fait mais je pense que l'on peut aboutir en suivant cette piste sachant que la définition de la convexité est la même :
pour tout
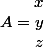\in\mathbb{R}^3)
,
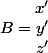\in\mathbb{R}^3)
et

,
B)\leq \lambda f\(A\)+(1-\lambda)f\(B\))
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 07 Juil 2008, 10:24
par sclormu » 07 Juil 2008, 10:24
Salut, étant de classe C^2 cette fonction sera convexe si et seulement si sa matrice hessienne est positive. Il te reste donc à calculer la matrice des dérivées secondes, et le signe de ses valeurs propres : trace et déterminant doivent être positifs.
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 07 Juil 2008, 10:30
par sclormu » 07 Juil 2008, 10:30
Oublie l'histoire de trace et det, j'avais pas vu le z. Ceci dit ça s'applique à une sous-matrice. Je trouve

-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 07 Juil 2008, 22:14
par MacManus » 07 Juil 2008, 22:14
Salut sclormu et merci !!
Effectivement en écrivant la Hessienne de f et en calculant son déterminant de telle sorte qu'il soit positif ou nul, j'obtiens bien la condition

.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 07 Juil 2008, 22:35
par nuage » 07 Juil 2008, 22:35
Salut,
dans le genre plus simple on peut aussi remarquer que
=(x+\frac12 y)^2+(a-\frac14)y^2+z^2)
Et le résultat devient assez facile à démontrer directement à partir de la définition.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 07 Juil 2008, 22:56
par MacManus » 07 Juil 2008, 22:56
Oui nuage tu as raison j'ai pensé au début réduire en somme de carrées...mais tu utilises quelle définition exactement pour démontrer le résultat...celle avec l'inégalité ? comment faire dans ce cas ?
En gros pour que f soit convexe, elle doit être une forme bilinéaire symétrique définie positive (un produit scalaire), cad à condition que

, ce qui se voit très clairement ici ok)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
