Géometrie

[frygorn]

Bonjour a toutes et à tous. J'ai un petit problème sur une question:

Determiner l'ensemble F des points M de E par lequels passe un et un seul plan Pm.

Pm:x+my-mz=1
E: ensemble des points de l'espace

Ce que j'ai fait c'est que j'ai cherché un point M(x,y,z) tel que il existe une unique solution m avec M appartenant à Pm.
cela revient à ce que x+my-mz-1=0 admette une unique solution en m .
Je trouve comme solution m=(1-x)/(y-z) y different de z
Mais je vois pas ce que ça represente alors si vous pouvez m'aider ça m'arrangerait.

[sclormu]

Salut. Tu as bien raisonné. Appelons U l'ensemble des points de l'espace par lesquels passe un et un seul plan .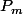

Si effectivement tu considères un point de coordonnées tel que 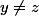alors il y a bien une unique valeur de m qui convient, celle que tu as calculé, donc ces points font tous partie de U.
Réciproquement, si tu considères un point tel que , regarde l'équation du plan 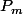: combien existe-t-il de valeurs de m telle que l'équation soit satisfaite ? Il y a une petite discussion à faire.

[frygorn]

Je vais voir la suite ,c'est la question suivante en fait^^ "quelle est la reunion des plans Pm lorques m decrit l'ensemble des réels"
Merci pour l'aide

[sclormu]

Cette question peut-être reformulée ainsi : pour quelles valeurs de x,y,z peut-on trouver m tel que l'équation soit satisfaite ?