Indépendance et dépendance linéaire

[ferrari24]

Deux vecteurs a et b de V2 sont linéairement indépendant si, quel que soit les réels A et B on a :
A a + B b = 0

Deux vecteurs sont dits linéairement dépendants si l'un d'eux au moins est une combinaison linéaire des autres.


Je ne vois pas comment à partir de la seconde "affirmation" on arrive à la deuxième. Je ne comprend pas pourquoi la somme de deux vecteurs linéairement indépendant vaut zéro

Aidez-moi!!!

[Zebulon]

Deux vecteurs a et b de V2 sont linéairement indépendants si, quels que soient les réels A et B on a :
A a + B b = 0

Cette affirmation est fausse!
Deux vecteurs a et b sont linéairement indépendants (dans un plan) si et seulement si:
s'il existe A et B deux réels tels que Aa+Bb=0, alors A=0 et B=0.
Tu comprends mieux?
Zeb.

[rene38]

Bonjour
ou bien
Deux vecteurs et de sont linéairement indépendants si, quels que soient les réels A et B non nuls tous les deux on a :

[danskala]

Salut,

deux vecteurs et sont linéairement indépendants si
quelquesoit les réels A et B, implique A=0 et B=0.
( , ) (*)

Deux vecteurs sont linéairement dépendants (ou liés) si
il existe deux réels A et B tels que et ou . (j'ai écrit la négation de la phrase (*))
Autrement dit,
Deux vecteurs sont linéairement dépendants (ou liés) si il existe un couple de réels tels que

En espérant ne pas trop t'embrouiller.

@+

[Zebulon]

Cette affirmation est fausse!
Deux vecteurs a et b sont linéairement indépendants (dans un plan) si et seulement si:
s'il existe A et B deux réels tels que Aa+Bb=0, alors A=0 et B=0.
Tu comprends mieux?
Zeb.

AAAAAAh :mur: j'ai fait une terrible erreur de quatificateur!(et merci aux autres de m'avoir corrigée):

Deux vecteurs a et b sont linéairement indépendants (dans un plan) si et seulement si:
quels que soient A et B deux réels tels que Aa+Bb=0, alors A=0 et B=0.

Voilà qui est mieux...

[ferrari24]

Merci pour vos réponses. Ces formules doivent-elles être apprises tel quel ou bien peut-on les démontrer. Je veux dire par là, que je n'aurais jamais pensé à ces formules pour déterminer si deux vecteurs sont linéairement dépendants ou indépendants, de quelle logique découlent-t-elles ?

:zen:

[Zebulon]

C'est la définition même de deux vecteurs linéairemant indépendants, qui se généralise en dimension supérieure (tu verras ça si tu fais de l'algèbre après la Terminale).
Cependant, tu peux voir que deux vecteurs et sont liés dans si et seulement s'ils vérifient, d'après la définition:
il existe deux réels a et b tels que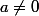 , , 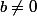et
ssi il existe deux réels a et b tous non nuls tels que
ssi et sont colinéaires, ce qui correspond plus à ce que tu appelles la logique! (moi, j'appellerais ça plutôt l'intuition ou l'image naturelle qu'on s'en fait).
J'espère que ça t'aidera à retenir cette formule.
A bientôt,
Zeb.