Polynomes

[arfa58]

Bonjour,
J'ai encore besoin de votre aide, à chaque fois vous m'aidez bien.
:happy2:


Soit A, B, C trois polynômes non nuls à coéfficients réels satisfaisant la relation :

A²+B²=C²

1. Montrer que si C a une racine réelle alpha, alors A(alpha) = B(alpha) = 0

Comment dois-je procéder ?

[le_fabien]

bonjour,
en commençant par poser C(alpha)=0

[sclormu]

bonjour,
en commençant par poser C(alpha)=0

C'est vrai que c'est assez balèze comme question.

[arfa58]

On est pas tous des bêtes en maths. :hum:

[Antho07]

On est pas tous des bêtes en maths. :hum:

Le post de sclormu est un peu déplacé....

Bon alors l'égalité A²+B²=C² est une égalité sur les polynomes, elle est donc valable pour n'importe quelle valeur auquel on évalue.

Autrement dit, pour tout x dans R, A(x)²+B(x)²=C(x)²

Maintenant Applique cette égalité à

et utilise le fait que est une racine de C, donc que

[le_fabien]

Laissons le chercher , je suis certain que arfa 58 va trouver maintenant. :++:

[Antho07]

Laissons le chercher , je suis certain que arfa 58 va trouver maintenant. :++:

Je pense que le probleme venait de comment interpreter le fait que A²+B²=C² soit une egalité sur les polynomes

[arfa58]

Merci pour vos réponses.
Oui le fait que ça soit des polynômes me perturbe.


C()=rac(A()²+B()²)

Si C()=0
alors rac(A()²+B()²)=0
A()²+B()²=0
A()²=B()²
A()=B()=0


C'est juste ça ? Ou je suis à coté ?

[leon1789]

Il ne faut pas oublier qu'on travaille dans R et que dans R, tout carré est p... ou nul.

[leon1789]

Oui le fait que ça soit des polynômes me perturbe.

Le fait que ce soit des polynômes n'a rien à voir avec la choucroute : on a le même résultat avec n'importe quelles fonctions de :
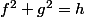
si et que alors .

[sclormu]

Oui, désolé.............. j'aurais pas du.
Toutes mes confuses, arfa58.

Pour me faire pardonner :

lemme.
si sont des réels, et que , alors .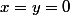

preuve.
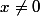
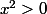
En effet, supposons par exemple que , alors et donc
, ainsi . Par contraposition on en déduit le résultat.

[arfa58]

Merci pour vos réponses. :jap:

Vous saurez peut-être m'aider pour :

Soit P un polynôme irréductible. Montrer que si P divise B et C, alors P divise A.

[abcd22]

Bonjour,
Si p divise b et c, alors a divise toute combinaison linéaire de b et c... (c'est vrai dans tous les anneaux).

[leon1789]

Soit P un polynôme irréductible. Montrer que si P divise B et C, alors P divise A.

Pourquoi toujours ajouter des hypothèses inutiles ?
Et puis il faut quand même connaitre la définition de "diviser"...

PS : montrer ce que dit abcd22, c'est exactement (non, je ne rigole pas...) calculer et dire que ça fait 0 !

[arfa58]

:help:

Si vous savez, ou avez de vraies pistes pour une démonstration "claire".

[leon1789]

Tu peux traduire P divise B par une certaine égalité ?

[arfa58]

Comment ça ?

[leon1789]

tiens, autre question :
un nombre pair + un nombre pair = un nombre .........

un multiple de P + un multiple de P = un ...................

C'est exactement pareil pour ta question !

[leon1789]

Comment ça ?

Pour toi, que signifie > ???

[ThSQ]

Thread surréaliste.