[Résolu] Changement de variable..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
arfa58
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Juin 2008, 14:16
-
 par arfa58 » 29 Juin 2008, 14:34
par arfa58 » 29 Juin 2008, 14:34
Salut !
Désolé de vous déranger (encore une fois !) Mais je bloque sur un petit énoncé..
Calculer la primitive :
y=e^(2x)/(rac(e^x+1)) en faisant le changement de variable t=rac(e^x+1)
avec rac() => racine carrée.
C'est le fait qu'il faille faire un changement de variable qui m'ennuie :triste:
Merci..
 par metaphysiconigologien » 29 Juin 2008, 14:47
par metaphysiconigologien » 29 Juin 2008, 14:47
Salut arfa58 !
C'est la bonne méthode pourtant je vois pas ce qui t'ennuies !
C'est la méthode classique quand on une racine dans l'intégrale ! Fais le et après, il n'y a plus de blocage.
Bon courage
-
arfa58
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Juin 2008, 14:16
-
 par arfa58 » 29 Juin 2008, 14:49
par arfa58 » 29 Juin 2008, 14:49
Merci pour ta réponse,
Je vois pas comment je dois procéder,
Tout à l'heure j'avais tan(x) j'ai trouvé tout de suite mais avec la racine :triste:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 29 Juin 2008, 14:52
par fatal_error » 29 Juin 2008, 14:52
Salut,
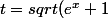\\<br />=>t^2=e^x+1\\<br />t^2-1=e^x\\<br />x=ln(t^2-1)\\<br />dx=\frac{2t}{t^2-1})
la vie est une fête

 par metaphysiconigologien » 29 Juin 2008, 14:56
par metaphysiconigologien » 29 Juin 2008, 14:56
Ben essaye de poser d'abord u = exp (x) puis t = rac(u+1)
 par metaphysiconigologien » 29 Juin 2008, 14:58
par metaphysiconigologien » 29 Juin 2008, 14:58
tu trouves normalement 2*[(rac(exp(x)+1)^5)/5 - ((rac(exp(x)+1)^3)/3]
-
arfa58
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Juin 2008, 14:16
-
 par arfa58 » 29 Juin 2008, 18:07
par arfa58 » 29 Juin 2008, 18:07
Je ne vois tjs pas comment on y arrive :doh:
 par metaphysiconigologien » 29 Juin 2008, 18:21
par metaphysiconigologien » 29 Juin 2008, 18:21
bon, tu fais le changement de variable t = rac ( exp(x) +1 ), tu as donc dx = 2*t*dt/(t^2-1). Ton integrale devient alors (t^2-1)*2t que tu sais intégrer puis il faut revenir en x !
Voila arfa58.
-
arfa58
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Juin 2008, 14:16
-
 par arfa58 » 29 Juin 2008, 18:46
par arfa58 » 29 Juin 2008, 18:46
metaphysiconigologien a écrit:bon, tu fais le changement de variable t = rac ( exp(x) +1 ), tu as donc dx = 2*t*dt/(t^2-1). Ton integrale devient alors (t^2-1)*2t que tu sais intégrer puis il faut revenir en x !
Voila arfa58.
C'est pas plutôt (t²-1)²/t ?
Mais justement une fois que j'ai ça, c'est dur à intégrer non ?
Merci bcp pour ton aide :happy2:
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 29 Juin 2008, 18:46
par Aspx » 29 Juin 2008, 18:46
Le changement de variable est
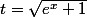
donc
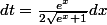
i.e
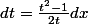
donc
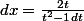
Ensuite on a
^2}{t} \frac{2t}{t^2-1^} dt = \int_{\sqrt{e^a+1}}^{\sqrt{e^x+1}} 2 (t^2-1) dt = 2 \left[ \frac{t^3}{3}-t \right]_{\sqrt{e^a+1}}^{\sqrt{e^x+1}} = 2\left(\frac{(e^x+1)^{\frac{3}{2}}}{3}-\sqrt{e^x+1}\right)+cte)
Une primitive est donc
^{\frac{3}{2}}}{3}-\sqrt{e^x+1}\right))
-
arfa58
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Juin 2008, 14:16
-
 par arfa58 » 29 Juin 2008, 18:49
par arfa58 » 29 Juin 2008, 18:49
Ah, il faut mettre des bornes comme ça..
Bah merci à vous 3 , maintenant je comprends :)
(désolé j'ai qu'un petit bac STI !)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
