Equation a 4 inconnues

[louloup1er]

Salut a tous, j'aimerais savoir comment résoudre une équation a 4 inconnues :
La voici :
7x + 4y + 1z + 3t = 157
3x + 2y + 4z + 8t = 145
9x + 5y + 1z + 2t = 184
4x + 6y + 4z + 7t = 186

[Mohamed]

salut;
tu peux écrire le système sous sa forme matricielle et chercher l'inverse de la matrice si elle est inversible...

[fatal_error]

Salut,

tu peux poser l'equation matricielle AX=B
avec :


et

Apres faut discuter sur le déterminant de A (une, infinité ou aucune solution) pis si detA!=0, tu as l'inversion qui est possible. cad
Tu peux aussi regarder du coté des méthodes de Cramer pour résoudre ton eq matricielle.

[leon1789]

Pour résoudre un système linéaire, il y a aussi la méthode du pivot (dite aussi méthode par substitution) : je crois que c'est plus élémentaire et économique que de calculer l'inverse d'une matrice ou des déterminants (la matrice n'est pas creuse ici). De préférence, prendre des pivots valant 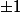bien sûr.

Quand on ne veut calculer la valeur de qu'une seule inconnue ou quand on fait du calcul en parallèle --> formules de Cramer.

Lorsque qu'il y a plusieurs systèmes du même type (AX=B, AX=C, etc) à résoudre --> calcul de l'inverse de A

[leon1789]

7x + 4y + 1z + 3t = 157
3x + 2y + 4z + 8t = 145
9x + 5y + 1z + 2t = 184
4x + 6y + 4z + 7t = 186

J'avoue que le membre de droite me fait peur !! (pas de courage pour faire des calcul avec des nombres à 3 ou 4 chiffres...)

[Clembou]

Pour résoudre un système linéaire, il y a aussi la méthode du pivot (dite aussi méthode par substitution) : je crois que c'est plus élémentaire et économique que de calculer l'inverse d'une matrice ou des déterminants (la matrice n'est pas creuse ici). De préférence, prendre des pivots valant bien sûr.

Quand on ne veut calculer la valeur de qu'une seule inconnue ou quand on fait du calcul en parallèle --> formules de Cramer.

Lorsque qu'il y a plusieurs systèmes du même type (AX=B, AX=C, etc) à résoudre --> calcul de l'inverse de A

Il y aura beaucoup de calcul pour le pivot de Gauss parce que la matrice n'a pas une forme spéciale (je dirais qu'il y aura plus de 10 calculs) mais ça me semble plus économique que de calculer l'inverse ou le déterminant...

[Aspx]

Comatrice et Sarrus, c'est bon pour le calcul mental :ptdr:

[leon1789]

Il y aura beaucoup de calcul pour le pivot de Gauss parce que la matrice n'a pas une forme spéciale (je dirais qu'il y aura plus de 10 calculs) mais ça me semble plus économique que de calculer l'inverse ou le déterminant...

Pas moins de 10... hum, allez, je me lance... :ptdr:

(1) : 7x + 4y + 1z + 3t = 157
(2) : 3x + 2y + 4z + 8t = 145
(3) : 9x + 5y + 1z + 2t = 184
(4) : 4x + 6y + 4z + 7t = 186



(1)
(2)
(4)
(5) = (3)-(1) : 2x + y - t = 27



(1)
(2)
(5)
(6) = (4)-(2) : x + 4y - t = 41



(1)
(2)
(6)
(7) = (6)-(5) : -x + 3y = 14



(7) : x = 3y - 14
(6) : t = 7y - 55
(1) : z = 157 - 7x -4y -3t = ... en fonction de y
(2) : 3x + 2y + 4z + 8t = 145 ... equation en y

je craque....

[abcd22]

Salut a tous, j'aimerais savoir comment résoudre une équation a 4 inconnues :
La voici :
7x + 4y + 1z + 3t = 157
3x + 2y + 4z + 8t = 145
9x + 5y + 1z + 2t = 184
4x + 6y + 4z + 7t = 186

La solution classique est la méthode de Gauss, mais il faut réfléchir un peu avant de l'appliquer, sinon on peut vite avoir des coefficients pas pratiques :
1) réordonner les équations et l'ordre des inconnues pour simplifier les calculs :
z + 4y + 7x + 3t = 157
z + 5y + 9x + 2t = 184
4z + 2y + 3x + 8t = 145
4z + 6y + 4x + 7t = 186
2) Éliminer les z des 3 dernières équations en leur soustrayant respectivement une, 4 et 4 fois la première ligne :
z + 4y + 7x + 3t = 157_
y + 2x - t = 27
-14y - 25x - 4t = -483
-10y - 24x - 5t = -442
3) Éliminer les y des 2 dernières équations en leur ajoutant respectivement 14 et 10 fois la 2e :
z + 4y + 7x + 3t = 157
y + 2x - t = 27
3x - 18t = -105
-4x - 15t = -213
4) Diviser la 3e ligne par 3 pour simplifier, puis ajouter 4 fois la 3e ligne à la 4e ligne pour éliminer x et trouver t, remonter les équations pour en déduire x, puis y, puis z.
5) Vérifier les résultats.