Series entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 25 Juin 2008, 15:51
par pouik » 25 Juin 2008, 15:51
Bonjour,
Je n'arrive pas du tout à résoudre l'exercice suivant, je ne vois même pas comment le demarrer. Pourriez vous m'aider ?
Merci d'avance. :zen:
" Donner le domaine de définition calculer S(x), avec :
 = \sum_{n=1}^{+\infty} (\frac{1-x}{x})^n + \sum_{n=1}^{+\infty} \frac{1}{n} \times (\frac{x+1}{x})^n)
"
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Juin 2008, 16:01
par Quidam » 25 Juin 2008, 16:01
pouik a écrit:Bonjour,
Je n'arrive pas du tout à résoudre l'exercice suivant, je ne vois même pas comment le demarrer. Pourriez vous m'aider ?
Merci d'avance. :zen:
" Donner le domaine de définition calculer S(x), avec :
 = \sum_{n=1}^{+\infty} (\frac{1-x}{x})^n + \sum_{n=1}^{+\infty} \frac{1}{n} \times (\frac{x+1}{x})^n)
"
Pour le domaine de définition, tu dois dire que :
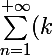^n)
est défini pour

, de même pour
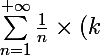^n)
Tu en tires les conséquences pour x.
Les deux sommes en question sont du cours, non ?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 25 Juin 2008, 16:22
par pouik » 25 Juin 2008, 16:22
Donc pour la première, on veut donc :
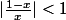
, soit :
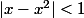
, soit :
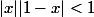
d'où : on trouve :
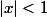
donc le rayon de convergence de la première série est

.
Par contre pour la deuxième je ne vois pas comment faire car la série de terme général

est divergente donc il faudrait que

dépende de

, mais ca ce n'est pas possible!! donc.... :mur: :mur:
Merci d'avance pour votre aide.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Juin 2008, 19:50
par fatal_error » 25 Juin 2008, 19:50
Bonjour,
pour la deuxième, je tenterais bien le critère de D'alembert :
=\Large \sum_{n=1}^{+\infty} \frac{1}{n} \times (k)^n)
CV si
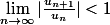
ce qui donne sauf erreur
}|<1)
avec
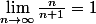
Edit: je viens de saisir le message de Quidam. Honte à moi de pas connaitre mon cours

.
la vie est une fête

-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 25 Juin 2008, 20:11
par pouik » 25 Juin 2008, 20:11
Honte à moi aussi, la deuxième vaut :-
)
non???
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Juin 2008, 20:36
par Quidam » 25 Juin 2008, 20:36
pouik a écrit:Donc pour la première, on veut donc :
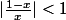
, soit :
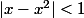
, soit :
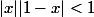
d'où : on trouve :
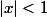
Ah oui ? Et si
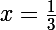
crois-tu que
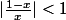
? Fais un peu le calcul, pour voir...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Juin 2008, 12:35
par pouik » 26 Juin 2008, 12:35
Bonjour,
En fait j'avais déterminé le domaine pour lequel on a : |x| < 1 et |1-x| < 1 et puis j'avais pris l'intersection des deux domaines, mais effectivement ca n'a pas l'air de marcher.
Comment faire alors ? Je ne vois vraiment pas comment avoir la condition recherchée.... :briques: :briques:
Merci d'avance pour votre aide.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 26 Juin 2008, 17:58
par Quidam » 26 Juin 2008, 17:58
[quote="pouik"]Bonjour,
En fait j'avais déterminé le domaine pour lequel on a : |x| 0
Je te laisse traiter la deuxième...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 26 Juin 2008, 18:02
par Quidam » 26 Juin 2008, 18:02
[quote="pouik"]Bonjour,
En fait j'avais déterminé le domaine pour lequel on a : |x| 1 suffisait pour que |a/b| < 1, sans que cela soit nécessaire ! Tu aurais alors trouvé une condition suffisante. Mais ta condition ( |a| <1 et |b|<1 ) n'est ni nécessaire, ni suffisante !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
"