re,
finalement, je trouve l'exo (niveau bac+1 ?) hyper intéressant à rédiger.
voili,voilou:
}{t} dt)
est une intégrale semi convergente.
en t=0, l'intégrande admet un prolongement par continuité. Tout se passe
comme si localement, on intégrait une fonction continue. non problemo.
la fonction f:
=\int_{x}^{+\infty} \frac{\sin(t)}{t} dt)
est donc bien définie sur
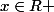
, continue et
=0)
On étudie maintenant l'intégrale
dx)
le but du jeu étant de montrer que c'est une intégrale semi-convergente,
en fait similaire à l'intégrande, qui est elle-même le reste d'une
intégrale semi-convergente :zen:
L'idée, c'est de formuler f, en primitivant par parties, mais pas avec la même
primitive :zen: sur l'intervalle

et sur l'intervalle
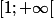
pour
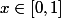
comme primitive de
)
, on choisit
)
d'où
=\frac{\cos(x)-1}{x}+\int_{x}^{+\infty} \, \frac{1-cos(t)}{t^2} dt)
f admet un prolongement par continuité en x=0, elle est bornée sur l'intervalle compact [0;1] et donc intégrable sur [0,1].
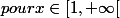
comme primitive de
)
, on choisit
)
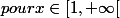
=\frac{\cos(x)}{x} - \int_{x}^{+\infty} \, \frac{\cos(t)}{t^2} dt)
encore une intégration par partie. On est en train de faire une sorte de DL
de f(x):
=\frac{\cos(x)}{x}+\frac{\sin(x)}{x^2} - 2 \int_{x}^{+\infty} \, \frac{\sin(t)}{t^3} dt)
Quand on intègre f sur
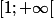
, le 1er terme donne une intégrale semi-convergente,le deuxième terme et troisième terme donnent chacun une intégrale absolument convergente.
conclusion: ce genre de démo est intéressante car elle permet d'inverser
des opérateurs que l'on pourrait qualifier de "semi-convergents"
