petite question :
Soit
Alors
Soit
Comment faire pour réduire Q sous formes de carré?
Forme quadratique, Gauss
11 messages
- Page 1 sur 1
Forme quadratique, Gauss
par fatal_error » 12 Juin 2008, 21:07
Bonjour,
petite question :
Soit=2xy)
Alors=\frac{(x+y)^2-(x-y)^2}{2})
Soit=2(xy+yz+zx))
Comment faire pour réduire Q sous formes de carré?
petite question :
Soit
Alors
Soit
Comment faire pour réduire Q sous formes de carré?
la vie est une fête 
par fatal_error » 12 Juin 2008, 21:18
Ben, pour q, j'ai remarqué "l'identité du parallèlogramme".
Mais je ne vois pas comment faire pour trois variables.
Enfin, si jamais j'essaye par exemple d'obtenir des carrés,
=(x+y+z)^2-x^2-y^2-z^2)
Le problème vient que j'ai 4 carré, donc yen a un qu'on pourrait forcément se passer mais je ne sais pas s'il y a une méthode, et l'intuition chez moi, c'est pas la gloire !
Mais je ne vois pas comment faire pour trois variables.
Enfin, si jamais j'essaye par exemple d'obtenir des carrés,
Le problème vient que j'ai 4 carré, donc yen a un qu'on pourrait forcément se passer mais je ne sais pas s'il y a une méthode, et l'intuition chez moi, c'est pas la gloire !
la vie est une fête
par Nightmare » 12 Juin 2008, 21:28
Et si tu écris par exemple :
(z+x)-x^{2})
On a donc :
=2(x+y)(z+x)-2x^{2})
et d'après le résultat précédent :
(z+x)-2x^{2}=\frac{(2x+y+z)^{2}-(y-z)^{2}}{2}-2x^{2})
:happy3:
On a donc :
et d'après le résultat précédent :
:happy3:
par sandrine_guillerme » 12 Juin 2008, 21:37
Salut fatal_error,
salut Nightmare,
pour fatal_error je te donne comment on fait :
par exemple :
q(x,y,z) = xy + yz +xz
on choisit un monome, ici par exemple, xy et on ecrit tous les monomes avec x et y
 = (x+z)(y+z) -z^2)
Astuce à connaître :
(y + z) = ( \frac{x + z + y + z}{2} ) ^2 - ( \frac{y + z- x- z}{2} ) ^2)
(ça vient de l'identite remarquable a²-b²)
tu réinjecte :
et t'obtiens :
 = (x + z)(y + z) = ( \frac{x + z + y + z}{2} ) ^2 - ( \frac{ y + z - x - z}{2} ) ^2 -z^2)
++
salut Nightmare,
pour fatal_error je te donne comment on fait :
par exemple :
q(x,y,z) = xy + yz +xz
on choisit un monome, ici par exemple, xy et on ecrit tous les monomes avec x et y
Astuce à connaître :
(ça vient de l'identite remarquable a²-b²)
tu réinjecte :
et t'obtiens :
++
par fatal_error » 12 Juin 2008, 21:52
Oki, j'ai bien compris.
Merci beaucoup à vous deux! :-)
Merci beaucoup à vous deux! :-)
la vie est une fête
par mathelot » 13 Juin 2008, 08:05
bjr à tous,
j'en profrite (bienvenue chez les cht'i) pour poser une petite question, n'ayant pas tout compris aux formes quadratiques:
cette décomposition dûe à Gauss permet d'écrire la forme quadratique
comme somme de carrés de formes linéaires indépendantes.
On obtient donc la signature. A ces formes
correspond une
base
de l'espace vectoriel telle que
=\delta_{i,j})
. C'est sa base duale.
mais si cette forme est liée à un produit scalaire, qu'on veut obtenir
une base orthonormée, l'idée naturelle (c'est à dire quand on a tout oublié) est de considérer la base duale des formes linéaires qu'on a trouvées avec la décomposition en somme de carrés.
manque de bol, la base duale n'est pratiquement jamais orthogonale.
c'est comme ça que je me suis retrouvé avec des équations d'ellipse
réduites à leur forme canonique, dans des repères du plan obliques.
Comment faire, il faut diagonaliser la matrice associée à la forme bilinéaire ?
Est ce qu'il y a un rapport avec la décomposition de Gauss ?
autre question:
si l'on récupère une équation
dans un repère oblique 
est-ce que c'est considéré comme une ellipse ?
j'en profrite (bienvenue chez les cht'i) pour poser une petite question, n'ayant pas tout compris aux formes quadratiques:
cette décomposition dûe à Gauss permet d'écrire la forme quadratique
comme somme de carrés de formes linéaires indépendantes.
On obtient donc la signature. A ces formes
base
mais si cette forme est liée à un produit scalaire, qu'on veut obtenir
une base orthonormée, l'idée naturelle (c'est à dire quand on a tout oublié) est de considérer la base duale des formes linéaires qu'on a trouvées avec la décomposition en somme de carrés.
manque de bol, la base duale n'est pratiquement jamais orthogonale.
c'est comme ça que je me suis retrouvé avec des équations d'ellipse
réduites à leur forme canonique, dans des repères du plan obliques.
Comment faire, il faut diagonaliser la matrice associée à la forme bilinéaire ?
Est ce qu'il y a un rapport avec la décomposition de Gauss ?
autre question:
si l'on récupère une équation
est-ce que c'est considéré comme une ellipse ?
par Antho07 » 13 Juin 2008, 12:21
La méthode de Gauss permet d'obtenir une base orthogonale pour ta forme quadratique.
Lorsque qu on fait la methode de gauss on obtient
=a_{1} L_{1}^{2}(x) +\ldots +a_{n}L_{n}^{2}(x))
ou les L1...Ln sont independants.
La base orthogonale est donnee par l'anteduale de de ces L1....Ln.
Commen trouver l'anteduale?
En inversant le systeme et en prenant la tranposee.
Ensuite si q est vient d 'un produit scalaire les a1...an sont tous positifs non nuls, on peut donc normer la base.
Comment faire??
Notons)
la base orthogonale trouvée, b la forme polaire de q.
et Posons}})
La base)
est normée et orthogonale d'ou le resultat.
La matrice de q dans cette base est la matrice In
Lorsque qu on fait la methode de gauss on obtient
ou les L1...Ln sont independants.
La base orthogonale est donnee par l'anteduale de de ces L1....Ln.
Commen trouver l'anteduale?
En inversant le systeme et en prenant la tranposee.
Ensuite si q est vient d 'un produit scalaire les a1...an sont tous positifs non nuls, on peut donc normer la base.
Comment faire??
Notons
et Posons
La base
La matrice de q dans cette base est la matrice In
par Antho07 » 13 Juin 2008, 12:44
sandrine_guillerme a écrit:
++
A partir de la il faut trouver l'anteduale.
Je reecris cela:
Bon ici, q ne provient pas d'un produit scalaire, il y a deux ai negatif, on pourra pas normer.
Recherchons l'anteduale, ecrivons
On inverse on obtient
on transpose on obtient
voila pour trouver l'anteduale.
calcule L1(f1), L2(f2) L3(f3)
L1(f2)... pour verifier
par Antho07 » 13 Juin 2008, 15:31
mathelot a écrit:Merçi Antho07,
Dans ton exemple ,l'antéduale n'est pas une base orthogonale,
car.
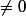
ce que j'avais déja constaté sur d'autres exemples.
là, on se retrouverait avec une équation de quadrique dans un repère oblique.
:hum:
Mais on obtient une base orthogonale pour q pas pour le produit scalaire.
Cependant sur un espace euclidien il doit exister une base a la fois orthogonale pour q et orthonormale pour .
Cela doit revenir a chercher les vecteurs propres de la matrice
pour le q de l'exemple
le Polynome caracteristique est
un vecteur propre associee à -1/2 est (0,1,-1).
un autre associee orthogonale et libre est (2,-1,-1).
un vecteur propre associee a 1 est ( 1,1 ,1)
verifions si la base { (0,1,-1), (2,-1,-1),(1,1,1)}convient
apperement ils sont orthogale pour
ici , q(x,y,z)=xy+xz+yz
donc
est sa forme polaire.
La base trouvée marche bien.
Le pourquoi du comment cela marche vient du fait que les espaces propres d'une endomorphisme autoadjoint sont orthogonales deux a deux.
Si B est une base orthonormee pour .
En notant M=Mat(b,B) (b la forme polaire de q)
alors l'endomorphisme f de E tels que Mat(f,B)=M (on regarde la matrice comme celle d'un endomorphisme).
alors f verifie pour tout x, y =b(x,y).
De plus c le seule f qui verifie cela.
Ensuite f est autoadjoint pour
cela veut dire que =.
Par un thoereme spectrale (plus sur du nom...bref) les espaces propres de f sont deux à deux orthogonaux pour
Mais en faite ils sont aussi orthogonaux pour q ( ie pour b).
en effet, si V et V' sont associe a L et L' deux valeurs propres differentes.
b(V,V')===L=0 car =0.
Ainsi une union de base orthoganale (pour ) de chaque espace propres formera une base orthogonales de E pour et pour q.
On peut de plus normee la base pour
En esperant avoir ete utile
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :