Topologie

par **jeje56** » 08 Juin 2008, 20:36

Bonsoir,

J'ai une petite question concernant cet exercice :

Pour (a,b) couple de

on note

l'application définie par :

MQ

est

-contractante

Je calcule |g(x,y)-g(x',y')| et j'arrive à :

et non

ce qui prouverait la contractance, est-ce la même chose ? La dernière accolade est-elle bien considérée comme un couple ?

Merci bcp d'avance...

par **jeje56** » 08 Juin 2008, 21:28

Personne ne peut m'aider ?... Merci à vous :-)

par **ThSQ** » 08 Juin 2008, 21:32

Ben tu as

avé X=(x,y) et Y(x',y') et basta

par **jeje56** » 09 Juin 2008, 10:40

Slt,

Mais

différent de |(x,y)-(x',y')|=|(x-x',y-y')| en termes de notations non ?

Merci à vous

par **yos** » 09 Juin 2008, 14:05

jeje56 a écrit:|(x-x',y-y')|

Norme euclidienne?

par **ThSQ** » 09 Juin 2008, 17:33

jeje56 a écrit:Mais différent de |(x,y)-(x',y')|=|(x-x',y-y')| en termes de notations non ?

Perso je comprends pas ce que tu veux dire. Je crois que tu cherches trop compliqué.

par **jeje56** » 09 Juin 2008, 18:04

Norme euclidienne ?

Non, valeur absolue...

Ce que je veux dire : est-ce que

différent de

?

Merci pour votre aide

par **augusto** » 09 Juin 2008, 19:44

jeje56 a écrit:Non, valeur absolue...

Ce que je veux dire : est-ce que
différent de ?

Merci pour votre aide

ben non à priori. Tout dépend de la norme que tu utilises ici. Ici tu peux prendre la norme L1(

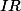
) et dans cette norme
||(x;y)|| = |x |+|y| et ainsi ||(x - x' ; y - y')|| = ||(y -y'; x - x')|| car N(a;b) = N(b;a). Donc tu peux et tu as terminé ton exercice

par **jeje56** » 09 Juin 2008, 20:07

Merci pour ta réponse, mais avec cette norme a-t-on bien :

||g(x,y)-g(x',y')||=

?

Topologie

Topologie

Qui est en ligne