Logarithme (ln) : petit problème
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 12:48
par DenisT » 08 Juin 2008, 12:48
Bonjour :we:
Je bloque sur un exercice qui semble pourtant simple mais que je n'arrive pas à résoudre :
Il faut faire la dérivée de ceci :
f(x) = ln (1-x)/(1+x)
La réponse est :
f'(x) = -2/(1+x)(1-x)
Je ne vois du tout comment arriver à cette réponse ! :hein:
Merci d'avance, et bon dimanche !
Denis
-
pronto
- Messages: 9
- Enregistré le: 06 Juin 2008, 00:18
-
 par pronto » 08 Juin 2008, 13:01
par pronto » 08 Juin 2008, 13:01
Ce n'est pas plutot f(x)= ln ( (1-x)/(1+x)) parce que dans ce cas, je trouve f'(x)= -2/ (1-x)(1+x)
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 13:07
par DenisT » 08 Juin 2008, 13:07
Oui oui, c'est bien ça, j'ai oublié les parenthèses.
Comment as-tu trouver la réponse alors ?
Merci ! :++:
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 08 Juin 2008, 13:10
par farator » 08 Juin 2008, 13:10
Salut,
Tu as juste à savoir que la dérivée de
)
c'est
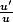
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 08 Juin 2008, 13:11
par farator » 08 Juin 2008, 13:11
Salut,
Ta fonction c'est :
f(x) = ln [(1-x)/(1+x)]
ou
f(x) = [ln (1-x)]/(1+x)
?
-
pronto
- Messages: 9
- Enregistré le: 06 Juin 2008, 00:18
-
 par pronto » 08 Juin 2008, 13:15
par pronto » 08 Juin 2008, 13:15
C'est plutot la première fonction Farator.
Il suffit juste de savoir que la dérivée de ln (u) est u'/u.
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 13:16
par DenisT » 08 Juin 2008, 13:16
C'est ceci :
ln ((1-x)/(1+x))
Donc le ln concerne bien tout ce qui suit après.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 08 Juin 2008, 13:21
par farator » 08 Juin 2008, 13:21
Ok, donc il suffit de savoir calculer la dérivée de (1-x)/(1+x)
Après tu sais que la dérivée de ln(u) c'est u'/u
Tout simple .. :++:
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 13:35
par DenisT » 08 Juin 2008, 13:35
Mmmmhh, j'ai beau essayer, même avec les formules et je n'arrive pas à la réponse donnée qui est f'(x) = -2/(1+x)(1-x)
Déjà, comment trouver le dénominateur ? Ca devrait être une division, non ?
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 08 Juin 2008, 13:37
par farator » 08 Juin 2008, 13:37
Bon,
commence par me dire quelle est la dérivée de (1-x)/(1+x)
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 13:44
par DenisT » 08 Juin 2008, 13:44
donc la formule est :
u/v = ( u'.v + u.v' ) / v²
-1.(1+x) - (1-x).1 / (1+x)²
-1-x-1+x / x²+2x
-2/x²+2x
C'est bien ça ?
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 08 Juin 2008, 13:45
par farator » 08 Juin 2008, 13:45
Cherche pas l'erreur plus loin :p
(u/v)' = ( u'.v - u.v' ) / v²
-
DenisT
- Messages: 6
- Enregistré le: 08 Juin 2008, 12:43
-
 par DenisT » 08 Juin 2008, 13:49
par DenisT » 08 Juin 2008, 13:49
Haaa j'ai trouvé !
Donc j'ai :
(-2/x²+2x) / ((1-x) / (1+x)) = (-2/(1+x)²) . ((1+x)/(1-x))
Et ensuite on simplifie.
J'allais trop loin avec le dénominateur au carré. Faut le laisser comme tel, pour pouvoir simplifier par après.
Merci beaucoup, ça m'a aider de le refaire :we:
Edit : ça ne venait pas de la formule. Dans l'exercice j'ai bien mis un - au lieu d'un +. ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
