Suite numérique: monotonie et convergence?

[alexii]

Bonjour,
On me demande dans un exercice de construire à l'aide de la courbe (H) = h(x)=(x+8)/(2x+1) définie sur [0;5] et de la droite d'équation y=x (donc solutions x=2 et x=-2) les points d'abscisses u0, u1, u2, u3 en expliquant leur construction.
Voici la suite numérique:
U0=1
Un+1 = (Un+8)/(2Un+1) , n appartenant à N
Donc j'ai trouvé u1=3, u2=11/7, u3=67/29
Par contre en faisant le graphique (avec le logiciel sinequanone) les points forment une spirale. (je n'ai jamais vu ça)
Comment expliquer la monotonie et la converge?

Merci beaucoup
a++

[MacManus]

Bonjour !

On a une suite définie par son 1er terme et la relation de réccurence 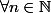. La fonction h est continue sur [0,5]. Pour connaître la monotonie de la suite u, tu étudies celle de la fonction h. En fonction de cette monotonie, tu cherches un majorant ou bien un minorant, pour pouvoir montrer la convergence...

j'espère que je ne dis pas de bêtises.

[alexii]

Merci beaucoup pour votre aide.

Sans vouloir abuser, j'ai une autre question:

Voici mon dilemme:

J'ai la suite:
U0=1
U(n+1)=(Un+8)/(2Un+1)

Ensuite j'ai la suite géométrique:
Vn= (Un-2)/(Un+2)
Après calcul cela me donne Vn= (-1/3)*(-3/5)^n
Je n'arrive pas à trouver Un après plusieurs essais
Quelqu'un pourrais me donner un indice?
Merci
A++