Questions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 10:03
par Chuck Nurris » 03 Juin 2008, 10:03
bonjour. j'ai plusieurs questions que je n'arrive pas resoudre. j'aimerais profiter de votre aide pour en trouver la solution.
je commence par la premiere :
)
est une fonction trois fois derivable sur

:
1/ montrer qu'il est possible de choisir le reel

de facon a ce que la fonction
=f(x)-f(a)-(1/2)(x-a)(f'(x)+f'(a))-A(x-a)^3)
puisse verifier le theoreme de Roll.
je sais que pour qu'une foonction puisse verifier le theoreme de Roll il faut que
=f(b))
. j'ai trouve que
=0)
mais impossible d'aller plus loin

merci d'avance.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 03 Juin 2008, 10:16
par Maxmau » 03 Juin 2008, 10:16
bj
Tu as déjà g(a) = 0
Choisis A de sorte que g(b) = 0
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 03 Juin 2008, 10:17
par Quidam » 03 Juin 2008, 10:17
Chuck Nurris a écrit:bonjour. j'ai plusieurs questions que je n'arrive pas resoudre. j'aimerais profiter de votre aide pour en trouver la solution.
je commence par la premiere :
)
est une fonction trois fois derivable sur

:
1/ montrer qu'il est possible de choisir le reel

de facon a ce que la fonction
=f(x)-f(a)-(1/2)(x-a)(f'(x)+f'(a))-A(x-a)^3)
puisse verifier le theoreme de Roll.
je sais que pour qu'une foonction puisse verifier le theoreme de Roll il faut que
=f(b))
. j'ai trouve que
=0)
mais impossible d'aller plus loin

merci d'avance.
Ben,
=f(b)-f(a)-(1/2)(b-a)(f'(b)+f'(a))-A(b-a)^3)
non ?
Donc, il suffit de choisir
-f(a)-(1/2)(b-a)(f'(b)+f'(a))}{(b-a)^3})
, non ?
Ou alors, j'ai mal lu !
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 10:36
par Chuck Nurris » 03 Juin 2008, 10:36
Quidam a écrit:Ben,
=f(b)-f(a)-(1/2)(b-a)(f'(b)+f'(a))-A(b-a)^3)
non ?
Donc, il suffit de choisir
-f(a)-(1/2)(b-a)(f'(b)+f'(a))}{(b-a)^3})
, non ?
Ou alors, j'ai mal lu !
non t'as pas mal lu :briques:
j'avoue que j'ai ete un peu bete la dessus. c'est juste que je cherchais plutot un raisonnement logique et pas mathematique de plus je suis vraiment saturé...(si je peux vous donner ca comme excuse).
j'ai une deuxieme question (qui j'espere la solution ne sera pas aussi evidente :doh: ). ca concerne les integrales.
on nous demande par un simple changement de variable montrer l'egalite suivante :
Cliquez ici pour la voir. j'ai posé
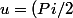-x)
. mais dans ce cas on trouvera l'egalite avec un moins (donc pas comme la consigne) :hein:
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 10:42
par Chuck Nurris » 03 Juin 2008, 10:42
edit: dsl pour le double poste.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 03 Juin 2008, 10:43
par Quidam » 03 Juin 2008, 10:43
Chuck Nurris a écrit:mais dans ce cas on trouvera l'egalite avec un moins (donc pas comme la consigne) :hein:
Eh non !
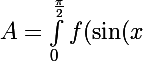)dx)
On pose, comme tu le suggères,
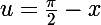
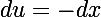
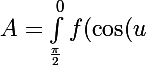)(-du)= \int_0^{\frac{\pi}{2}} f(\cos(u))(du)= \int_0^{\frac{\pi}{2}} f(\cos(x))(dx))
Voilou !
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 11:05
par Chuck Nurris » 03 Juin 2008, 11:05
Quidam a écrit:Eh non !
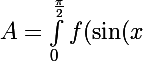)dx)
On pose, comme tu le suggères,
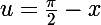
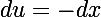
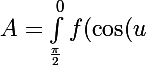)(-du)= \int_0^{\frac{\pi}{2}} f(\cos(u))(du)= \int_0^{\frac{\pi}{2}} f(\cos(x))(dx))
Voilou !
merci beaucoup. ca m'a encore echapé je ne sais plus ce qui m'arrive :triste:
j'aurais d'autres questions (j'ai une synthese demain). j'espere te trouver encore :++: merci bcp
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 14:11
par Chuck Nurris » 03 Juin 2008, 14:11
j'ai une autre question que je n'arrive pas a retrouver


cette fois-ci je ne crois pas avoir fait d'erreurs :
voici les formules! ils nous demandent de prouver que
)
est egale a comme mentionée (au cas ou c'est pas tres visible, je precise que l'integrale va de 0 a x).
voici mes etapes de resolution :
-
Page 1-
Page 2 merci pour votre aide.
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 20:56
par Chuck Nurris » 03 Juin 2008, 20:56
svp j'aimerais si c'est possible une indication. j'en ai besoin avant demain.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Juin 2008, 21:21
par Monsieur23 » 03 Juin 2008, 21:21
Bonjour.
C'est peut être trop tard, mais il suffit de vérifier que la fonction donnée est la primitive de (1+x²)^(3/2) qui s'annule en 0.
Je commence : Elle s'annule en 0.
A ton tour.
( Sinon, la flemme de regarder tes calculs, surtout à cette heure ci )
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Chuck Nurris
- Membre Naturel
- Messages: 55
- Enregistré le: 26 Déc 2007, 19:04
-
 par Chuck Nurris » 03 Juin 2008, 21:57
par Chuck Nurris » 03 Juin 2008, 21:57
Monsieur23 a écrit:Bonjour.
C'est peut être trop tard, mais il suffit de vérifier que la fonction donnée est la primitive de (1+x²)^(3/2) qui s'annule en 0.
Je commence : Elle s'annule en 0.
A ton tour.
( Sinon, la flemme de regarder tes calculs, surtout à cette heure ci )
ahhh ouii il suffit alors juste de deriver, et montrer que la dérivée est egale a la fonction qui sous l'integrale.
vraiment merci beaucoup. ce probleme me dérangeait beaucoup. :++:
moi ce que j'ai essaye de faire c'est de completement integrer la fonction.... je n'arrete pas de faire des catastrophes en ce moment... :triste:
a bientot.....pour l'algebre (synthese mardi prochain) lol
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 04 Juin 2008, 16:19
par Quidam » 04 Juin 2008, 16:19
Monsieur23 a écrit:Bonjour.
C'est peut être trop tard, mais il suffit de vérifier que la fonction donnée est la primitive de (1+x²)^(3/2) qui s'annule en 0.
Je commence : Elle s'annule en 0.
A ton tour.
( Sinon, la flemme de regarder tes calculs, surtout à cette heure ci )
Merci à Monsieur23 d'avoir pris le relais !
Chuck Nurris, désolé ! Je ne suis pas connecté en permanence, et en plus, à 12H30 hier, mon PC m'a lâché. Je ne sais toujours pas pourquoi, ni pourquoi il semble fonctionner à nouveau normalement... Mais ce n'est pas ton problème, c'est le mien. Heureusement, Monsieur23 était là !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
est une fonction trois fois derivable sur
:
de facon a ce que la fonction
puisse verifier le theoreme de Roll.
. j'ai trouve que
mais impossible d'aller plus loin

non ?
, non ?