Le problème de la Racine carrée

[moutonjr]

Bonsoir,
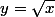
Je m'imaginais et sa courbe qui s'aplatissait... alors je me suis mis à l'étudier dans ma tête, et là j'ai eu un gros problème :


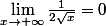
donc il existe une asymptote horizontale de au voisinage de (la courbe est plate car la dérivée est nulle.)

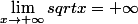
Or, , je ne comprends pas.

C'est tous simplement illogique, on sait que tôt ou tard la courbe s'aplatit comme , mais l'AHorizontale ne serait pas un ??


MODIFICATION : oui j'ai oublié de dire que peut-être que si une courbe a une pente plate (au voisinage de ) elle n'avolue plus du tout et donc a une valeur finie...

[Nightmare]

Bonsoir !

Aïe grosse erreur ! Aucun rapport entre la limite de la dérivée et les asymptotes !

Tout ce que tu as montré, c'est qu'effectivement les tangentes vont avoir tendance à s'aplatir, ie que la courbe va croître de plus en plus doucement, mais on peut croître doucement jusqu'à l'infini.

Tu prends la fonction ln, c'est encore pire que la racine.

[bombastus]

Bonsoir,
Je m'imaginais et sa courbe qui s'aplatissait... alors je me suis mis à l'étudier dans ma tête, et là j'ai eu un gros problème :


donc il existe une asymptote horizontale de au voisinage de (la courbe est plate car la dérivée est nulle.)

Qu'est ce qui te permet de dire qu'il y a une asymptote horizontale?
La limite que tu donnes montres que le nombre dérivé (donc le coeff directeur de la tengente) va tendre vers 0 mais sans l'atteindre.

Pour avoir une équation horizontale, il faut :
et non la limite de f' !

[moutonjr]

Aïe grosse erreur ! Aucun rapport entre la limite de la dérivée et les asymptotes !

Ah bon?? alors quand la dérivée est nullle, la courbe est plate, donc elle n'augmente plus du tout : comme 1/x elle croitra mais viendra un moment où elle croîtra tellement lentement qqu'elle approchera une valeur, non?

on peut croître doucement jusqu'à l'infini.

c'est là que ça me choque c'est qu'au voisinage de la courbe soit carrément plate, ie elle ne croit plus du tout!!

Tu prends la fonction ln, c'est encore pire que la racine.

C'est pas faux!

[Nightmare]

Sauf que la dérivée n'est pas nulle, elle tend vers 0 mais n'est pas nulle, c'est là toute la différence.

[moutonjr]

Sauf que la dérivée n'est pas nulle, elle tend vers 0 mais n'est pas nulle, c'est là toute la différence.

Euu..ba alors au voisinage de l'infini qu'est-ce qu'on a? un nombre fini puisque la courbe est plate???

[Nightmare]

eh bien au voisinage de l'infini on a que la courbe est de plus en plus plate comme je l'ai dit, mais elle n'est jamais plate, donc crôit toujours.

[moutonjr]

ahhh d'accord en fait je commence à comprendre... a n'importe quelle valeur qu'on se fixe elle passera au dessus.... Elle ne ressemble pas à 1/x qui croit aussi toujours mais qui approche une valeur mais c'est pas simple à se visualiser l'une par rapport à l'autre elles se ressemblent...
En tout cas merci vous m'ôtez d'un doute