J'ai besoin d'indications pour un probleme que j'ai travailler pendant 10 jours.
Voici l'enonce: Soit f une fonction differentiable a variable reelle definie sur une boule ouverte de

de centre
)
et de rayon

tel que

sur toute la boule ouverte.
Montrer qu'il existe une fonction unique

a variable reelle definie sur la boule ouverte
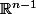
de centre

tel que
= g(x_1, \ldots,x_{n-1})
et que g est differentiable .
Je sais que une boule ouverte est connexe, donc f est constante par rapport la derniere variable

en utilisant le theoreme des accoissements finis, mais j'ai des difficultes de construire la fonction

proprement et de le montrer que c'est differentiable .
voici la definition que nous utilisons dans le cours:
f est differentiable en
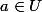
s'il existe

tel que
-f(a)-c_1(x_1-a_1)-\ldots c_n(x_n-a_n | { |x_1-a_1| +\ldots + |x_n -a_n|} =0)
En fait toutes les normes sont equivalentes sur

, donc je peux remplacer cette derniere par

mais j'ai pas reussi a eliminer le terme

sur le denominateur pour montrer la differentiabilite de

, on a

par hypothese car

.
