Variables aléatoires

[Maseru]

Bonjour à tous,

Une agence de location de voitures dispose pour ses clients de voitures classées en n (n>1) catégories. On suppose que n clients se présentent à cette agence pour louer chacun d'eux une voiture. Ces n clients choisissent de manière équiprobable la catégorie de la voiture qu'ils vont louer et le choix de chacun de ces n clients est indépendant du choix des autres.
Dans chaque catégorie il y a n voitures à louer.
Soit Xi la variable aléatoire égale au nombre de voitures louées dans la catégorie i et Yn la variable égale au nombre de catégories de voitures non louées.


je trouve que pour tout i, Xi suit une loi binomiale de paramètres (n;1/n)

mais il me faut trouver la loi de [somme de i=1 à n-1 des Xi] et je ne sais pas du tout comment faire; merci de votre aide

[Sa Majesté]

Si j'ai tout compris :
Pour tout i

Tu cherches la loi de

Et comme Xn suit une loi binomiale, n-Xn suit aussi une loi binomiale de paramètres (n;1-1/n)

[Maseru]

comment sais-tu que [somme de i=1 à n-1 des Xi] = n-Xn

[Sa Majesté]

Je n'ai peut-être pas tout compris alors :hum:
Il me semblait que puisqu'il y a n clients, alors la somme des Xi vaut n

[nuage]

Salut,

je trouve que pour tout i, Xi suit une loi binomiale de paramètres (n;1/n)

je suis d'accord mais il y a un point important à remarquer : les ne sont pas indépendantes.

mais il me faut trouver la loi de [somme de i=1 à n-1 des Xi] et je ne sais pas du tout comment faire

Sa Majesté t'a donné la réponse, mais je ne vois pas pourquoi tu en as besoin. Sauf si c'est pour répondre à une question que tu n'as pas écrite.


Pour la loi de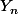 : on cherche à classer les applications de dans lui même suivant le nombre d'éléments de l'image. Toutes les applications sont équiprobables et il y en a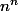
On a donc :

• 
• Il y a applications d'un ensemble à éléments dans un ensemble à éléments. Et façons de choisir un sous ensemble à éléments.
  D'où
• etc...

A+