Calcul d'un produit
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Luchir
- Messages: 8
- Enregistré le: 19 Fév 2008, 21:36
-
 par Luchir » 17 Mai 2008, 13:46
par Luchir » 17 Mai 2008, 13:46
svp aidez moi à calculé le produit suivant :
)
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 17 Mai 2008, 14:01
par nonam » 17 Mai 2008, 14:01
Bonjour, tu devrais pouvoir y arriver en t'aidant du polynôme :
^n-1)
-
Jean_Luc
- Membre Relatif
- Messages: 158
- Enregistré le: 25 Avr 2008, 10:17
-
 par Jean_Luc » 17 Mai 2008, 14:04
par Jean_Luc » 17 Mai 2008, 14:04
Salut,
Peut-être comme ça ?
^{\frac{1}{n}})
puis Euler...
-
Luchir
- Messages: 8
- Enregistré le: 19 Fév 2008, 21:36
-
 par Luchir » 17 Mai 2008, 16:07
par Luchir » 17 Mai 2008, 16:07
Merci j'ai trouvé la réponse :
Dans le cas général pou z complexe on a les égalités suivantes :
)
=
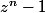
et
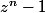
=
(z^{n-1}+z^{n-2}+....+z+1))
or
)
=
)
Pour z=1
)
=
)
finalement
)
=


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2008, 17:22
par leon1789 » 17 Mai 2008, 17:22
Jean_Luc a écrit:Peut-être comme ça ?
^{\frac{1}{n}})
oula attention : :id:
^{\frac{1}{n}}<br />= ({e^{i2\pi}})^{\frac{k}{n}} = 1^{\frac{k}{n}} = 1)
Donc toute racine n-ième de l'unité vaut 1 :zen:
-
Jean_Luc
- Membre Relatif
- Messages: 158
- Enregistré le: 25 Avr 2008, 10:17
-
 par Jean_Luc » 17 Mai 2008, 18:08
par Jean_Luc » 17 Mai 2008, 18:08
leon1789 a écrit:oula attention : :id:
^{\frac{1}{n}}<br />= ({e^{i2\pi}})^{\frac{k}{n}} = 1^{\frac{k}{n}} = 1)
Donc toute racine n-ième de l'unité vaut 1 :zen:
Pas dans C :lol3:
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 17 Mai 2008, 18:13
par nonam » 17 Mai 2008, 18:13
Jean_Luc a écrit: ^{\frac{1}{n}})
C'est la fonction puissance 1/n qui n'a pas de sens dans C...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2008, 18:15
par leon1789 » 17 Mai 2008, 18:15
oui, cette formule
Jean_Luc a écrit: ^{\frac{1}{n}})
n'est pas valable dans C. :lol3:
-
Jean_Luc
- Membre Relatif
- Messages: 158
- Enregistré le: 25 Avr 2008, 10:17
-
 par Jean_Luc » 17 Mai 2008, 18:16
par Jean_Luc » 17 Mai 2008, 18:16
nonam a écrit:C'est la fonction puissance 1/n qui n'a pas de sens dans C...
Je vois pas pourquoi,

non ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2008, 18:17
par leon1789 » 17 Mai 2008, 18:17
nonam a écrit:C'est la fonction puissance 1/n qui n'a pas de sens dans C...
oui on peut dire ça,
ou bien on dit que la fonction z -> z^(1/n) a un sens, mais elle n'a pas cette propriété (pourtant habituelle sur R).

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2008, 18:19
par leon1789 » 17 Mai 2008, 18:19
Jean_Luc a écrit:Je vois pas pourquoi,

non ?
ben il faut se décider :

? car une fonction ne donne qu'une image à un élément donné.
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 17 Mai 2008, 18:22
par nonam » 17 Mai 2008, 18:22
leon1789 a écrit:ou bien on dit que la fonction z -> z^(1/n) a un sens, mais elle n'a pas cette propriété (pourtant habituelle sur R).
Quelle sens lui donne-t-on ? On privilégie une racine parmi les n possible ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2008, 18:32
par leon1789 » 17 Mai 2008, 18:32
nonam a écrit:On privilégie une racine parmi les n possible ?
oui : on la prend d'argument le plus petit possible dans [0, 2 Pi[ par exemple. (il faut une détermination de l'argument, ou de la fonction logarithme.)
Et c'est du fait d'avoir une définition "bizarre" comme celle-là que des propriétés vraies sur R deviennent fausses sur C.
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 17 Mai 2008, 18:41
par nonam » 17 Mai 2008, 18:41
D'accord. Merci pour l'info, je n'en avais jamais entendu parler...
-
Jean_Luc
- Membre Relatif
- Messages: 158
- Enregistré le: 25 Avr 2008, 10:17
-
 par Jean_Luc » 17 Mai 2008, 18:46
par Jean_Luc » 17 Mai 2008, 18:46
OK merci pour les précisions.
Mon idée pour l'exo c'etait en fait de garder le

sans faire de supposition sur la racine n-ième de 1 dans C et esperer que cette expression se simplifie avec une autre puissance du genre

mais bon ça marche probablement pas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
