Bonsoir, il faut que je fasse mon deuil sur une question de dénombrement :
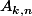
désigne l'ensemble des applications de |[1,k]| dans |[1,n]|,
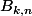
celui des applications surjectives de |[1,k]| dans |[1,n]|, son cardinal est noté
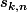
.
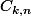
est l'ensemble des applications f de |[1,n]| dans

telles que
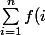=k)
.
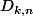
est le sous-ensemble de
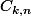
formé des f telles que
\ge 1)
pour tout i de |[1,n]|.
Pour n, k entiers naturels et
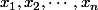
réels on a :
^k=\sum_{f \in C_{k,n}}\frac{k!}{f(1)! \cdots f(n)!}x_1^{f(1)}\cdots x_n^{f(n)}=\sum_{\varphi \in A_{k,n}}x_{\varphi (1)}\cdots x_{\varphi (k)})
La question est : montrer que pour
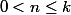
on a
! \cdots f(n)!})
Je me doute qu'il faut appliquer le lemme des bergers avec une application bien choisie de
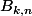
dans
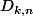
mais je vois pas trop laquelle...(je suis pas très doué là-dedans)
Cette question provient de l'épreuve de Maths II MP de l'X de cet après-midi... j'en tremble encore xD
Merci d'avance aux bonnes âmes qui pourront m'éclairer

