Petit problème intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gaway
- Messages: 2
- Enregistré le: 13 Mai 2008, 19:30
-
 par gaway » 13 Mai 2008, 19:35
par gaway » 13 Mai 2008, 19:35
Je suis en pleines révisions du bac, je sèche sur une question d'annale, plus précisément sur la réponse donnée par le corrigé...
Je voudrais savoir pourquoi l'intégrale de x à x+1 de 1/(x+1) est précisément égale à 1/(x+1)... J'ai du mal à me le représenter.
J'espère avoir été assez clair, merci d'avance.
Maxime.
-
Taupin sur Lyon
- Membre Relatif
- Messages: 233
- Enregistré le: 27 Oct 2007, 18:57
-
 par Taupin sur Lyon » 13 Mai 2008, 19:43
par Taupin sur Lyon » 13 Mai 2008, 19:43
gaway a écrit: l'intégrale de x à x+1 de 1/(x+1) est précisément égale à 1/(x+1)...
Tu es sur que c'est l'intégrale de x à x+1 de dx/(x+1) ?? c'est le même x donc ?
-
gaway
- Messages: 2
- Enregistré le: 13 Mai 2008, 19:30
-
 par gaway » 13 Mai 2008, 20:27
par gaway » 13 Mai 2008, 20:27
Taupin sur Lyon a écrit:Tu es sur que c'est l'intégrale de x à x+1 de dx/(x+1) ?? c'est le même x donc ?
En réalité c'est l'intégrale de n à (n+1) de dx/(n+1), pour tout n appartenant à N*
La variable est n.
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 13 Mai 2008, 20:38
par bombastus » 13 Mai 2008, 20:38
Bonsoir,
si c'est l'intégrale de n à (n+1) de dx/(n+1),
la variable d'intégration c'est x. On a alors
intégrale de n à (n+1) de dx/(n+1) = intégrale de n à (n+1) de dx
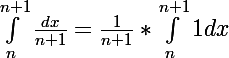
Et il ne reste plus qu'à calculer l'intégrale.
-
Taupin sur Lyon
- Membre Relatif
- Messages: 233
- Enregistré le: 27 Oct 2007, 18:57
-
 par Taupin sur Lyon » 13 Mai 2008, 20:38
par Taupin sur Lyon » 13 Mai 2008, 20:38
ah ! je préfère ça !
edit : réponse donnée ci dessus ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
