Matrice et base

[rougedemoiselle]

Bonjour,

Pouvez vous corriger ?

Soit E l'espace vectoriel des réels des polynômes à coefficient réels de degré au plus 2 et C={1,X,X²} la base canonique de E.

On considère l'endomorphisme f de E défini par :

et id l'application identique de E.
1/ Ecrire la matrice A de l'application f relativement à la base C et calculer la matrice M de l'application f²=fof relativement à la base C.
A=
M=

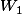
2/ Calculer les rangs des applications f²+Id et f²-Id et donner des base B1 et B2 de chacun des sous-espces vectoriels = kerf(f²+Id) et W2= kerf(f²-Id)
Montrer que E= et que est une base B de E.
Par contre pour cette question pouvez vous m'aider ?

Merci

[jeje56]

On considère l'endomorphisme f de E défini par :

...

[rougedemoiselle]

...

Oh je suis vraiment désolée.

défini par :

[nyth]

1/ je suis d'accord
2/Avec les matrices de ces applications il est simple de déterminer la dimension du noyau, il ne reste plus qu'à appliquer le théorème du rang. Pour le reste, t'as une proposition qui dit que E = W1 + W2 (en somme directe) <=> l'intersection de W1 et W2 = {0} et dim W1 + dim W2 = dim E