Produit scalaire et hauteurs

[Steve49]

Bonjour,
J'aurais besoin d'aide pour un exercice.

Exercice :
Soit ABC un triangle.
AB = 7 cm
AC = 8 cm
BC = 10 cm
L est le milieu de [AB], M est le milieu de [AC] et N est le milieu de [BC].

Déterminer n tel que la hauteur issue de C soit : MA carré – MB carré = n.

[Benjamin]

Bonjour,

Pour la première question, la réponse est juste. Mais tu n'as pas donné ta démonstration, je ne peux donc pas te dire que tu as déterminé correctement, mais le fait que tu es la bonne réponse est déjà un bon point :).
Pour la suite, la hauteur issu de C, c'est la droite perpendiculaire au côté opposé à C et passant par C. Tu sais déjà que ton ensemble de points est perpendiculaire à (AB). Il reste à prouver que C appartient à cet ensemble.
Remplace M par C pour le vérifier.

[Steve49]

En effet je n'ai pas mis toute ma démonstrations pour la question 1 ) a) car elle était beaucoup trop longue mais je pense qu'elle est correct.
Donc pour la question b) je remplace comme tu me la di C par M et je trouve donc bien 45 à la fin mais j'aimerais savoir comment j'explique pourquoi je fait ça? je dis que l'ensemble de points est la hauteur issue de C dans le triangle ABC passe obligatoirement par le point C?
Pourrais tu m'expliquer les autres questions stp ?

[Benjamin]

Deux droites sont soient parallèles, soient confondues, soient sécantes en 1 point et un seul.
Deux droites parallèles qui ont un point en commun sont confondues et sont donc les mêmes.
Par définition de la hauteur, elle passe par C et est perpendiculaire à (AB).
Le lieu géométrique que tu as déterminé à la question 1), il est perpendiculaire à (AB).
Deux droites perpendiculaires a une même 3ème sont parallèles. Ainsi, la hauteur et la droite de la question 1 sont parallèles. Le point C vérifie l'équation. Donc C appartient et à la droite de la question 1, et à la hauteur (qui passe forcément par C), donc la hauteur et la droite de la question 1 sont les mêmes.

Pour la suite, tu écris que et tu utilises l'identité remarquable . Ensuite, n'oublie que K est le milieu de BC, et introduit le projeté de M sur (BC).

[Steve49]

Ok merci pour tes explications.

Pour la c) tu m'a dit de calculer MB carré - MC carré mais ce n'est pas plutôt MA carré - MC carré qu'il faut calculer ?
Si c'est ça j'ai fait le calcul et j'arrive à :
(vecteur JA + vecteur JC) . vecteur CA

[Benjamin]

Non, c'est une erreur d'énoncé. C'est MB²-MC²=-56. En fait, il faut refaire les questions a) et b) avec l'autre sommet c'est tout. Je t'ai donné une méthode qui marche bien, mais il suffit que tu reprennes la démonstration que tu as faite pour a) et ça marche :).

Ma méthode sera plus adéquate pour les questions suivantes, où c'est général.

[Steve49]

Oui en effet, c'est un erreur d'énocé (je n'avais pas fait attention en écrivant l'énoncé... ma prof a fait une erreur ^^).
D'accord donc si faut refaire comme la a) j'y arrive donc je refait sa tout de suite.

[Steve49]

Oui en effet, c'est un erreur d'énocé (je n'avais pas fait attention en écrivant l'énoncé... ma prof a fait une erreur ^^).
Donc en suivant ta méthode j'ai trouvé (vecteur KB + vecteur KC) . vecteur BC (ce résultat me parît incorrect)

[Steve49]

Oui en effet, c'est une erreur d'énoncé (je n'avais pas fait attention en écrivant l'énoncé... ma prof a fait une erreur ^^).
Donc en suivant ta méthode j'ai trouvé (vecteur KB + vecteur KC) . (2vecteurMK + vecteur KB + vecteur KC) (ce résultat me paraît incorrect)

[Benjamin]

Je t'écris la première ligne du calcul, ensuite, n'oublie pas que si K et le milieu de BC, alors .

.
Ensuite, démontre que .

Mais encore une fois, tu peux utiliser la même méthode que tu as faite précédemment !!! Prends celle qui te convient. Tu peux faire tout l'exo avec ce que tu as fait à la question a) et b)
En fait, la question c), c'est a) + b) avec un autre sommet, et la question d), c'est la question c) avec le dernier sommet, c'est tout. C'est juste que je pense la méthode que je te montre est la plus rapide et la plus élégante.

[Steve49]

Avec ta méthode, j'ai démontrer que vecteurMB + vecteur MC = 2MK :
MBcarré - MC carré = (vecteur MB - vecteur MC) . (vecteur MB + vecteur MC)
= (vecteur MK + vecteur MB + vecteur MK + vecteur KC).(vecteur MB + vecteur MC)
= 2MK . (vecteur MB + vecteur MC)

Avec ma méthode :
Ensemble des points M tels que MB carré – MC carré = - 28 est la droite perpendiculaire à (AB) et passant par L (L = projeté orthogonal sur (BC)) tel que IL = - 14/3 cm).
Ensuite AB carré - AC carré = 5carré - 9 carré = -56
Donc cet ensemble de points est la hauteur issue de A dans le triangle ABC.

[Benjamin]

Tu as fait une petite erreur en reprenant ma méthode.
Mais si tu as démontré proprement que l'

Ensemble des points M tels que MB carré – MC carré = - 28 est la droite perpendiculaire à (AB) et passant par L (L = projeté orthogonal sur (BC)) tel que IL = - 14/3 cm).

, ta méthode est très bien.
Je finis juste la mienne pour que tu vois, et j'en profite donc pour corriger ta petite erreur :
car K est le milieu de [BC].
Ensuite,
. Or l'ensemble des points M tel que , c'est bien la droite perpendiculaire à (CB) tel que .
La barre au-dessus indique que c'est des grandeurs algébriques. Ca permet de savoir si L est à droite où à gauche du milieu K.

J'en profite d'ailleurs pour te dire que IL=-14/3, c'est faux. En effet c'est . IL écrit comme ça, ça doit toujours être positif, car c'est une longueur.

[Steve49]

Donc pour la d) :
Ensemble des points M tels que MA carré – MC carré = 5,5 est la droite perpendiculaire à (AB) et passant par L (L = projeté orthogonal sur (AC)) tel que IL = 5,5/9 cm).
Ensuite AB carré - BC carré = 5carré - 6 carré = -11 (Or j'ai MA carré - MB carré = 11, serait -ce encore une faute de l'énoncé?)
Donc cet ensemble de points est la hauteur issue de B dans le triangle ABC.

Pour les dernière questions, je les ferais demain et je te marquerai mes résultats.
Je regarderais demain ta méthode et j'essayerai de faire les dernières questions avec.
En tout cas, merci beaucoup pour ton aide !

[Benjamin]

De rien,
Regarde bien le dernier post de la première page, je viens de le modifier. Je t'y ai montré une petite imprécision de ta part par rapport aux longueurs algébrique et réelle.

[Steve49]

J'ai utilisé ta méthode (je te marque que la fin des calculs) :
I - d) 2vecteur MJ . vecteur CA = 11
barre LJ = 11 / 18
L = projeté orthogonal sur (AC).

II - a) I milieu de [AB]
2vecteur MI . vecteurAC = k
barre LI = k / 2c

b) K milieu de [BC]
2vecteur MK . vecteur BC = k
barre LK = k / 2a

c) J milieu de [AC]
2vecteur MJ . vecteur AC = k
barre LJ = k / 2b

Pour la d je ne vois pas comment faire.

[Benjamin]

Je réalise après coup que c'est encore plus simple que ça. On sait que l'ensemble des points M tel que MA²-MB²=k, c'est la droite perpendiculaire à (AB) passant par H (projeté de C sur (AB)) tel que c'est-à-dire tel que .

Pour que cette droite soit la hauteur, il faut et il suffit que C appartiennent à cet ensemble, comme je te l'ai déjà dit avant (2 droites sont confondues, parallèle ou sécante, 2 droites perpendiculaire à une même droite sont parallèles ou confondues, point commun confondues).

Autrement dit, il faut et il suffit que AB²-AC²=k et donc k=c²-b².
Je ne vois pas de question d) pour la question 2).
A plus,

[Steve49]

J'avais oublié de marquer la question d) , je l'ai rajouté dans le premier topic.
Sinon les résultats que j'ai trouvé juste au dessus et que je t'ai marqué dans le topic d'avant sont corrects ?

[Benjamin]

Les résultats de ton topic précédent ne sont pas tout à fait juste (tu fais une erreur de signe) et en plus, ce n'est pas ce qu'on te demande. On te demande d'exprimer k en fonction de a, b et c. En fait, la longueur LI importe peu ici. Lis bien mon précédent topic. Je m'étais un peu emballé, et fait, c'est plus simple que ça. La relation vectorielle que nous avons montré permet de dire qu'on a une droite perpendiculaire au côté opposé du triangle, donc parallèle à la hauteur. Il suffit de faire passer cette droite par le sommet qui nous intéresse pour obtenir k. La dernière question est assez simple. Si H est le point d'intersection des 2 premières hauteur, il vérifie les deux relations vérifiées pour tout M (par exemple HA²-HB²=...).

Il faut et il suffit alors de vérifier que la relation est aussi vrai pour la dernière hauteur.

[Steve49]

Je viens de relire ton topic et tes explications pour les questions à partir de II - a) mais je ne comprends pas vraiment. Pourrais tu s'il te plaît me les réexpliquer?
Je me suis douté après coup que ce que je faisais pour le II - ce n'était pas ça car je refaisais la même chose qu'au grand I.

[Benjamin]

Ok. Donc, nous avons montré pour résoudre la question I, que :

Pour tout points A et B du plan, l'ensemble des points M tel que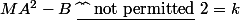 est égal à l'ensemble des points M tel que , où I est le milieu de [AB] et H le projeté orthogonal de M sur (AB).

Nous avons donc démontré que l'ensemble des points M tel que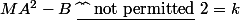 est une droite perpendiculaire à (AB) (appelons la (d)) (d'ailleurs, tu l'avais déjà démontré avec ta méthode. En fait, la façon de le montrer importe peu, ce qui compte, c'est seulement ce dernier résultat (en gras)).
Nous savons que la hauteur du triangle ABC issue de C est la droite perpendiculaire à (AB) et passant par C (appelons la (h)).
(d) et (h) sont perpendiculaire à une même droite ((AB) ici) donc (d) et (h) sont parallèles ou confondues. Pour que (d) et (h) soient une seule et même droite, il suffit donc que (d) passe par C. Or, si C appartient à (d), alors C vérifie la condition vérifiée par tous points M de la droite (d), à savoir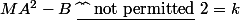 . Pour trouver k, il suffit donc de ??