Relation de récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 06 Mai 2008, 22:03
par rougedemoiselle » 06 Mai 2008, 22:03
Bonjour,
Pouvez vous m'aider ?
Soit n un entier non nul et x un nombre réel.
On pose :
)
=

^n})
Etablir une relation de récurrence entre
)
et
 (x))
On pourra effectuer une intégration par parties
Merci !
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 06 Mai 2008, 22:18
par Skullkid » 06 Mai 2008, 22:18
Bonsoir, fais l'intégration par parties classique :
^n}=1\times \frac{1}{(1+t^2)^n})
Qu'est-ce qui te bloque ?
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 08 Mai 2008, 13:40
par rougedemoiselle » 08 Mai 2008, 13:40
Skullkid a écrit:Bonsoir, fais l'intégration par parties classique :
^n}=1\times \frac{1}{(1+t^2)^n})
Qu'est-ce qui te bloque ?
Bonjour,
tout me bloque.
Alors j'écris ce que j'ai fait :
La formule d'intégration par parties :
g'(x) dx = f(x)g(x)-\Bigintf'(x)g(x))
Avec f(x)=
^n})
et f'(x)=
}{(1+t^2)^2})
g'(x)=1 et g(x)=x

(x)=
^n})
x+2n

^2})
dt
Je ne pense pas que ça soit correcte.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 08 Mai 2008, 15:25
par Skullkid » 08 Mai 2008, 15:25
Tu t'es embrouillée dans tes variables. Ici la variable d'intégration c'est t, pas x. Donc tes f et g sont fonctions de la variable t :
=\frac1{(1+t^2)^n} \ f'(t)=-\frac{2nt}{(t^2+1)^{n+1}})
=1\ g(t)=t)
D'où
=\frac{x}{(1+x^2)^n}+2n\int_0^x \frac{t^2}{(1+t^2)^{n+1}}dt)
Maintenant, tu dois trouver un lien entre l'intégrale du membre de droite et les

. L'astuce à utiliser est d'écrire
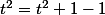
.
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 08 Mai 2008, 16:48
par rougedemoiselle » 08 Mai 2008, 16:48
Skullkid a écrit:Tu t'es embrouillée dans tes variables. Ici la variable d'intégration c'est t, pas x. Donc tes f et g sont fonctions de la variable t :
=\frac1{(1+t^2)^n} \ f'(t)=-\frac{2nt}{(t^2+1)^{n+1}})
=1\ g(t)=t)
D'où
=\frac{x}{(1+x^2)^n}+2n\int_0^x \frac{t^2}{(1+t^2)^{n+1}}dt)
Maintenant, tu dois trouver un lien entre l'intégrale du membre de droite et les

. L'astuce à utiliser est d'écrire
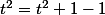
.
le lien que je trouve entre l'intégrale et les In est :

-
)
Je ne vois rien d'autres
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 08 Mai 2008, 21:50
par Skullkid » 08 Mai 2008, 21:50
J'ai pas compris ta réponse (fautes de frappe LaTeX ?). Enfin toujours est-il qu'il est impossible que tu aies du t hors d'une intégrale, t est la variable d'intégration, elle est muette.
Tu fais comme je t'ai dit :
^{n+1}}dt=\int_0^x \frac{t^2+1}{(1+t^2)^{n+1}}dt-\int_0^x \frac1{(1+t^2)^{n+1}}dt)
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 08 Mai 2008, 22:20
par rougedemoiselle » 08 Mai 2008, 22:20
Skullkid a écrit:J'ai pas compris ta réponse (fautes de frappe LaTeX ?). Enfin toujours est-il qu'il est impossible que tu aies du t hors d'une intégrale, t est la variable d'intégration, elle est muette.
Tu fais comme je t'ai dit :
^{n+1}}dt=\int_0^x \frac{t^2+1}{(1+t^2)^{n+1}}dt-\int_0^x \frac1{(1+t^2)^{n+1}}dt)
In(x)=
^{n+1}}dt)
-
)
????
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 08 Mai 2008, 22:27
par Skullkid » 08 Mai 2008, 22:27
Non, c'est pas

qui est égal à ça, lis un peu mes posts...et tu verrais pas un moyen de rapprocher l'autre intégrale d'une

?
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 08 Mai 2008, 22:56
par rougedemoiselle » 08 Mai 2008, 22:56
Skullkid a écrit:Non, c'est pas

qui est égal à ça, lis un peu mes posts...et tu verrais pas un moyen de rapprocher l'autre intégrale d'une

?
 = \frac{x}{(1+x^2)^n} + 2n[\Bigint^x _0 \frac{t^2 +1}{(1+t^2)^(n+1)}dt - U_(n+1)])
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 08 Mai 2008, 23:03
par Skullkid » 08 Mai 2008, 23:03
Voilà, tu y es presque. Maintenant, trouve un lien entre
^{n+1}}dt)
et
)
, et tu auras ta relation de récurrence.
PS : pour les indices et exposants en LaTeX, tape-les entre accolades {}, ça rend mieux.
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 08 Mai 2008, 23:18
par rougedemoiselle » 08 Mai 2008, 23:18
Skullkid a écrit:Voilà, tu y es presque. Maintenant, trouve un lien entre
^{n+1}}dt)
et
)
, et tu auras ta relation de récurrence.
PS : pour les indices et exposants en LaTeX, tape-les entre accolades {}, ça rend mieux.
^{n+1}}dt)
et
)
=
^(n+1)}dt + \Bigint^x _0 \frac{t^2}{(1+t^2)^(n+1)}dt)
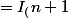 + [\frac{-1}{2n}\frac{t}{(1+t)^n}]^x _0 + \frac{In}{2n})
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 09 Mai 2008, 00:21
par Skullkid » 09 Mai 2008, 00:21
J'avoue ne pas comprendre grand-chose à ce que tu fais...
^{n+1}}dt=I_n(x))
, tout simplement, car

.
Bref, au final, ça nous fait :
=\frac{x}{(1+x^2)^n}+2n\int_0^x \frac{t^2}{(1+t^2)^{n+1}}dt=\frac{x}{(1+x^2)^n}+2n(I_n(x)-I_{n+1}(x)))
D'où ta relation de récurrence. Revois tout cet exercice à tête reposée depuis le début, il n'a rien de difficile et les méthodes utilisées (intégration par parties pour trouver une relation de récurrence, astuce du t²= t²+1-1, etc) reviennent assez souvent. Essaye aussi de comprendre la logique derrière tes calculs...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
. L'astuce à utiliser est d'écrire
.