Densité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 05 Mai 2008, 16:57
par aure555 » 05 Mai 2008, 16:57
Bonsoir, j'ai du mal à me lancer dans l'exercice suivant :
Trouver la densité de la somme de deux variables aléatoires indépendantes ayant une loi de probabilité de densité

pour

réeel.
Pourriez-vous m'aider à démarrer?
Merci
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 05 Mai 2008, 21:15
par aure555 » 05 Mai 2008, 21:15
Personne n'a une piste pour moi?
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 05 Mai 2008, 21:36
par Youcef » 05 Mai 2008, 21:36
Salut !
je te laisse ce message pour que tu ne te sens pas seul !! j'essaye depuis 10mn de trouver la solution , c'est vraie que c'est pas évident! (enfin j'espère car sinon, c'est sur que je vais rater mon éxam la semaine prochaine !) je te fais signe si j'ai quelque chose !
Ps : de ton coté, tu essaye bien la méthode de la fonction muette non ?
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 05 Mai 2008, 21:43
par Youcef » 05 Mai 2008, 21:43
Dis moi , est ce qu'il n'y aurait pas un domaine que tu aurais oublié de mentionner ?? parce que c'est ça qui me bloque , si on avait des condition sur X et Y ça serait très facile !
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Mai 2008, 05:43
par Dyo » 06 Mai 2008, 05:43
Salut,
Trouver la densité de la somme de deux variables aléatoires indépendantes ayant une loi de probabilité de densité \frac{1}{2} e^{-|x|} pour x réeel.
Connais-tu le produit de convolution ?
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 06 Mai 2008, 09:18
par aure555 » 06 Mai 2008, 09:18
Youcef a écrit:Dis moi , est ce qu'il n'y aurait pas un domaine que tu aurais oublié de mentionner ?? parce que c'est ça qui me bloque , si on avait des condition sur X et Y ça serait très facile !
Non je n'ai rien oublié dans l'énoncé.
Non mais je me suis renseigné sur Wikipedia (pour convolution)
Il faut 2 fonctions pour cela non?
Pourrais-tu m'en dire un peu plus?
Merci
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 06 Mai 2008, 17:31
par aure555 » 06 Mai 2008, 17:31
Bonjour,
dans ce cas-ci le produit de convolution est-il égale à

?
Ceci détermine la moyenne des deux fonctions?
Merci
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 06 Mai 2008, 19:23
par aure555 » 06 Mai 2008, 19:23
Bonjour,
dans ce cas-ci le produit de convolution est-il égale à

?
Ceci détermine la moyenne des deux fonctions?
Merci
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 06 Mai 2008, 20:53
par aure555 » 06 Mai 2008, 20:53
Bonjour,
dans ce cas-ci le produit de convolution est-il égale à

?
avec comme variable aléatoire x et t
Comment puis-je alors utiliser ceci pour résoudre l'énoncé?
Merci
-
Youcef
- Membre Naturel
- Messages: 60
- Enregistré le: 22 Mar 2008, 14:19
-
 par Youcef » 06 Mai 2008, 21:03
par Youcef » 06 Mai 2008, 21:03
Salut Aure ..
le produit de convolution est bien celui ci , mais je ne trouve pas non plus comment résoudre ce problème !!!!
personnellement, j'ai jamais fais de convolution, j'ai regardé quelques cours sur le net, mais je trouve rien de concret pour appliquer .. donc Désolé !!
une dernière chose :
avec comme variable aléatoire x et t
la par contre je suis pas d'accord avec toi !! on intègre par rapport a t et on considère x comme paramètre si tu veux .. mais c'est surement pas des variables aléatoires !!
j'espère que quelqu'un d'autre pourras te venir en aide !! a +
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 07 Mai 2008, 05:51
par Dyo » 07 Mai 2008, 05:51
Salut,
dans ce cas-ci le produit de convolution est-il égale à

?
C'est bien ça. En fait la densité de la loi somme de deux variables aléatoires indépendantes à densité est le produit de convolution des deux densités.
Ainsi si

est la densité de la v.a.
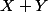
(de même densité que tu as énoncée), alors
=\frac{1}{4} \int_{-\infty }^{+\infty} e^{-|x-t|}e^{-|t|}dt<br />=\frac{1}{4}(\int_{-\infty}^x e^{-(x-t)}e^{-|t|}dt +\int_{x}^{+\infty}e^{x-t}e^{-|t|}dt))
Ensuite tu peux distinguer les cas où

est positif, négatif, je pense. Et l'intégrale devient facile à calculer en sortant les

.
Edit : Pour montrer ca
C'est bien ça. En fait la densité de la loi somme de deux variables aléatoires indépendantes à densité est le produit de convolution des deux densités.
Tu peux utiliser la méthode de la fonction borélienne, la connais-tu ?
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 07 Mai 2008, 16:26
par aure555 » 07 Mai 2008, 16:26
Bonjour,
j'ai traité les deux cas :
Pour x > 0 :
h(x) =
} + \frac{1}{4} \int_{0}^{x} e^{-t} e^{-(x-t)} + \frac{1}{4} \int_{x}^{+\infty} e^{-t} e^{-(x-t)})

=


=
)
Dans le cas où x < 0 , j'obtien quasi le même à savoir :
)
Plus exactement c'est identique à quelque signe près donc on a que h(x) =
)
La densité de la somme est donc égale à ceci alors? (moyennant les erreurs de calculs de ma part)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
?