Simplifier une dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
jejedu33
- Membre Naturel
- Messages: 25
- Enregistré le: 29 Déc 2005, 17:58
-
 par jejedu33 » 03 Mai 2008, 15:51
par jejedu33 » 03 Mai 2008, 15:51
Bonjour à tous,
J'ai la fonction f(x) =

D'où F'(x) =

c'est bien ça ?
Le problème, c'est que j'ai essayé de simplifier cette écriture, et j'arrive à :
f'(x) =

Mais cela ne semble pas être bon... quelqun peut m'aider a trouver mon erreur ?
Merci.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 03 Mai 2008, 16:37
par le_fabien » 03 Mai 2008, 16:37
Je pense que tu as mal réduit au même dénominateur.
Pour moi f'(x)=...
-
jejedu33
- Membre Naturel
- Messages: 25
- Enregistré le: 29 Déc 2005, 17:58
-
 par jejedu33 » 04 Mai 2008, 10:02
par jejedu33 » 04 Mai 2008, 10:02
Oups, je me suis trompé :
j'ai mis f'(x) = D'où F'(x) =

mais c'est f'(x) = D'où F'(x) =

Pas contre, LEFAB11, est-ce que tu peux détailler tes calculs, car même en partant du premier je n'y arrive pas... :hum:
Merci beaucoup.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 04 Mai 2008, 11:04
par Sa Majesté » 04 Mai 2008, 11:04
Ta dérivée est fausse
Déjà il te manque un facteur 2 car
' = n\, u'\, u^{n-1})
' = {(1+x^2)^{(\frac{1}{2})}}')
' = \frac{1}{2}\, 2x\, (1+x^2)^{(-\frac{1}{2})})
Mais ce n'est pas la seule erreur ...
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 04 Mai 2008, 11:30
par le_fabien » 04 Mai 2008, 11:30
Oui c'est vrai j'ai juste vérifié la réduction au même dénominateur et non la dérivé elle même.il y a plus qu'une erreur.
-
jejedu33
- Membre Naturel
- Messages: 25
- Enregistré le: 29 Déc 2005, 17:58
-
 par jejedu33 » 04 Mai 2008, 13:04
par jejedu33 » 04 Mai 2008, 13:04
SaMajestée, cela revient au même ce que j'ai fais, mais c'est plus pratique ta technique (en plus je me suis planté, u est égal à rac(1+x²) -1 et non pas rac(1+x²))
C'est bon j'ai une dérivée juste (vérifié à la calculette) :
f'(x) =
^-\frac{1}{2} - \sqrt{1+x^2}+1}{x^2})
Mais je ne parvient pas à simplifier tout ça...

Merci.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 04 Mai 2008, 16:28
par Sa Majesté » 04 Mai 2008, 16:28
Ca se simplifie un peu en multipliant haut et bas par
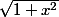
-
jejedu33
- Membre Naturel
- Messages: 25
- Enregistré le: 29 Déc 2005, 17:58
-
 par jejedu33 » 04 Mai 2008, 18:35
par jejedu33 » 04 Mai 2008, 18:35
Merci finalement j'ai laissé comme ça car après cela m'arrange.
Merci à tous.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 04 Mai 2008, 18:52
par le_fabien » 04 Mai 2008, 18:52
J'ai une dérivée positive ou nulle.Vous aussi ? :ptdr:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 04 Mai 2008, 19:25
par Sa Majesté » 04 Mai 2008, 19:25
Qui ? Moi ? Oui ! :ptdr:
Et toi jejedu33 ? Raconte un peu ...
-
jejedu33
- Membre Naturel
- Messages: 25
- Enregistré le: 29 Déc 2005, 17:58
-
 par jejedu33 » 04 Mai 2008, 20:00
par jejedu33 » 04 Mai 2008, 20:00
Oui affirmatif. Et c'est confirmé par la courbe de la fonction F qui est toujours croissante. Mais moi j'étudie la fonction sur ]0;+inf[ donc elle est toujours positive sur cet intervalle.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités