Asymptote question

[Alex77]

Bonjour,
je voulais savoir si une fonction pouvait admettre une asymptote oblique ( donc d'équation y = ax+b ) dont la limite de la différence ( lim f(x)-(ax+b) ) pouvait être égale à 2 ? ( habituellement égale à 0 )

Soit, est-ce possible que lim f(x)-(ax+b) = 2 peut être pris en compte comme asymptote oblique de la fonction f?

[Nicolas_75]

Euh...
si f(x)-(ax+b) -> 2
Alors f(x)-(ax+b+2) -> 0
donc l'asymptote est y=ax+(b+2)

[Alex77]

Et si je vois à la calculette que l'équation de la droite donnée est juste? :s

C'est la fonction f(x)= racine(1 + x²) - 1
et il demande si la droite d'équation y = x -1 est asymptote

[Nicolas_75]

Il n'y a pas de 2 dans cette histoire !

f(x)-(x-1)
= (racine(1 + x²) - 1) - (x-1)
= racine(1 + x²) - x --> 0 (multiplier par la quantité conjuguée)

[becirj]

La limite en + l'infini de est 0

[Alex77]

Je me suis trompé de formule à copier ^^' mais c'est bon, j'ai trouvé mon érreur, par contre il y a une question qui succède :
Démontrer que quel que soit le réel x, 1+|x| <(ou égal) racine(1+x²)

[Nicolas_75]

Ce résultat me semble faux.
Prends x=1
2 =< V2 ?

[Alex77]

Tu as raison, c'est étrange.. par contre pour tout x € R-{1} ca a l'air de marcher

[Nicolas_75]

Bien sûr. Prends x=0,9 par exemple.

[rene38]

Bonjour

....

[Alex77]

Rene, l'inégalité doit être vérifiée pour tout x € |R

[Galt]

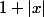
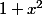
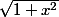
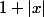
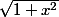
Ton inégalité est fausse quel que soit le réel x. Le carré de vaut est toujours supérieur à , le carré de . Les nombres positifs et étant dans le même ordre que leurs carrés, on a pour tout réel x :
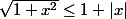
, le contraire de ce que tu veux démontrer.

[rene38]

il y a une question qui succède :
Démontrer que quel que soit le réel x, 1+|x| <(ou égal) racine(1+x²)

Dans mon message de 16h03, je démontre que (me semble-t-il) :
quel que soit le réel non nul x, l'inégalité est fausse !

[Alex77]

L'énoncé est faux, ca va faire plaisir à quelqu'un ca :) merci :)