Polynome dans Z[X]
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Avr 2008, 18:41
par aviateurpilot » 26 Avr 2008, 18:41
salut
soit

et
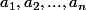
tel que:
i)
=1)
ii)
)
montrer que
\subset a_j\mathbb{Z})
bn chance
(dans ma solution, j'ai pas utilisé le (i) ,donc ma solution est fausse ou bien (i) n'est pas une condition nessecaire)
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 01 Mai 2008, 11:25
par BiZi » 01 Mai 2008, 11:25
aviateurpilot a écrit:salut
soit

et
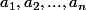
tel que:
i)
=1)
ii)
)
montrer que
\subset a_j\mathbb{Z})
bn chance
(dans ma solution, j'ai pas utilisé le (i) ,donc ma solution est fausse ou bien (i) n'est pas une condition nessecaire)
Salut,

sont les coefficients du polynôme? S'ils sont quelconques c'est faux! Ils suffit de prendre un polynôme dont tous les coefficients sont égaux à

, et un peu n'importe quoi pour les autres

tant qu'ils sont premiers avec

; en 0 il risque de y'avoir un problème.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 02 Mai 2008, 13:39
par aviateurpilot » 02 Mai 2008, 13:39
BiZi a écrit:Salut,

sont les coefficients du polynôme? S'ils sont quelconques c'est faux! Ils suffit de prendre un polynôme dont tous les coefficients sont égaux à

, et un peu n'importe quoi pour les autres

tant qu'ils sont premiers avec

; en 0 il risque de y'avoir un problème.
dzl, j voualais ecrire
\subset a_j\mathbb{Z})
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 03 Mai 2008, 10:41
par BiZi » 03 Mai 2008, 10:41
Dans ce cas il existe

tel que
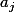
divise
)
pour une infinité de

. En utilisant les polynômes interpolateurs de Lagrange, on peut exprimer P sous la forme
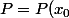*L_0+P(x_1)*L_1+...+ P(x_n)*L_n)
avec
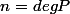
, et
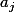
qui divise
)
pour tout
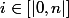
. On a alors P inclus dans
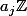
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Mai 2008, 11:53
par aviateurpilot » 03 Mai 2008, 11:53
BiZi a écrit:Dans ce cas il existe

tel que
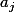
divise
)
pour une infinité de

. En utilisant les polynômes interpolateurs de Lagrange, on peut exprimer P sous la forme
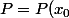*L_0+P(x_1)*L_1+...+ P(x_n)*L_n)
avec
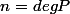
, et
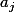
qui divise
)
pour tout
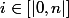
. On a alors P inclus dans
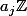
.
je pense que c'est faux car deja pour n'importe quel polynome
|P(x_0+kP(x_0)),)
donc
)
divise P(x) pour une infinité de x et comme on a pas forcement
)
divise P(x) pour tt x
car
)
peux etre dans
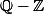
.
donc on a pas forcement
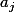
|P=P(x_0)*L_0+P(x_1)*L_1+...+ P(x_n)*L_n
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 03 Mai 2008, 20:11
par ThSQ » 03 Mai 2008, 20:11
aviateurpilot a écrit:i)
=1)
Juste pour être sûr : c'est bien le le pgcd
global, les a_i ne sont pas a priori premiers entre eux deux à deux ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Mai 2008, 20:34
par aviateurpilot » 03 Mai 2008, 20:34
oui, le pgcd golobal,
mais j'ai pas utilisé (i) dans ma solution lol.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Mai 2008, 12:17
par aviateurpilot » 18 Mai 2008, 12:17
je posterai ma solution apres 7jrs,
bn chance
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Mai 2008, 18:41
par aviateurpilot » 30 Mai 2008, 18:41
definition: on dit que
\in\mathbb{Z}[X]\times \mathbb{Z}^n)
est gentille si
)
si
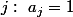
alors
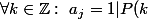)
sinon on a
>1)
on considere alors la suite
)
dans l'ensemble des gentilles tel que
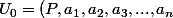)
si
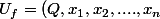)
avec
>1)
on prend
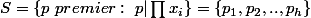
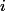
tel que
)
(
je vous laisse montrer cela)
on prend alors
}))
qui est bien
gentille.finallement on peux remarque que pour un certain
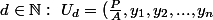)
tel que
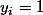
pour un certain

et d'apres la construction on doit avoir
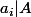
.
donc
.)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
et
sont les coefficients du polynôme? S'ils sont quelconques c'est faux! Ils suffit de prendre un polynôme dont tous les coefficients sont égaux à
, et un peu n'importe quoi pour les autres
tant qu'ils sont premiers avec
; en 0 il risque de y'avoir un problème.
tel que
divise
pour une infinité de
. En utilisant les polynômes interpolateurs de Lagrange, on peut exprimer P sous la forme
avec
, et
qui divise
pour tout
. On a alors P inclus dans
.
est gentille si