Calcul d'integrale

[quaresma]

bonjour à tous,
dans l'ensemble, j'ai compris comment calculer une integrale.
Cependant, je ne me rappel plus comment faire pour calculer une integrale de ce style :

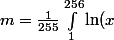pourriez-vous m'aider?
merci bcp pour vos réponses

[mathelot]

par parties

[The Void]

(u=ln(x), v'=1)

[quaresma]

par parties

on est obligé de le faire par parties ?
si oui, peux-tu me faire une ptite demo STP ? :id:

[trocho]

ln(x)=1*ln(x)

Tu poses u'(x)=1, v(x)=ln(x).
On a donc u(x)=x et v'(x)=1/x

Et tu appliques la formule d'intégration par parties.

[quaresma]

l'integration par parties n'est pas au programme de mon bts (info de gestion)...

[nonam]

Comme The Void l'a écrit, utilise alors le fait que est un primitive de ln.

[quaresma]

et je dois faire quoi du 1/255 ?

[nonam]

ben tu calcules la valeur de l'intégrale, et tu multiplies par

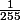
[julian]

Comme The Void l'a écrit, utilise alors le fait que est un primitive de ln.

Cette méthode ne doit pas vraiment être utilisée en générale (vu qu'on peut aussi bien poser u=x que u=x-1, et parfois poser u=x-1 ça arrange beaucoup de choses)

Sinon un petit rappel sur les intégrales s'impose:



où: est une constante
est UNE primitive de

(donc ici et )

[quaresma]

Sinon un petit rappel sur les intégrales s'impose:



où: est une constante
est UNE primitive de

(donc ici et )

'lut julian,
donc si j'aurai pris une fonction plus simple nous amenant à l'intégrale ci-dessous:



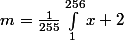
Ca aurait donné:


c'est bien cela ?

[quaresma]

un pti up pour une ptite aide :)

[nonam]

c'est bien ça, si m=
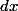
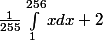
Mais comme tu n'as pas mis de , ton m aurait pu aussi être qui n'a pas la même valeur.
Il faudrait donc faire attention à l'écriture...

[quaresma]

ok je ferai attention merci pour ta reponse ;)