Endomorphisme et récurrence

[yocto]

Bonjour,

J'ai besoin de votre aide pour résoudre l'exercice suivant :

Soit E un K espace vectoriel et f un endomorphisme de E.
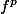
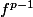
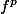
On suppose que ker f = ker f². Soit p>=2 et x ker, je dois montrer que x ker et ensuite en déduire que pour tout p1, ker = ker f (en posant la récurrence).

Merci de m'aider

[Maxmau]

Bonjour,

J'ai besoin de votre aide pour résoudre l'exercice suivant :

Soit E un K espace vectoriel et f un endomorphisme de E.
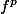
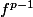
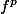
On suppose que ker f = ker f². Soit p>=2 et x ker, je dois montrer que x ker et ensuite en déduire que pour tout p1, ker = ker f (en posant la récurrence).

Merci de m'aider

Bj

Rem :On a toujours Ker f^p contenu dans Ker f^(p+1)
Hyp : Kerf = Kerf²
Si x est dans Kerf^3 , f(x) est dans Kerf² mais Kerf² = Kerf donc x est dans Kerf² =Kerf
...etc...

[alavacommejetepousse]

bonjour c'est vrai pour p = 1 ( et 2)

on le suppose pour p on le montre pour p+1

soit x dans ker f^(p+1) on a f^p(f(x)) = 0 finir la preuve