Bonjour,
je dois calculer deux intégrales:
intégrale de 0 à pi de ((x^2)*sin(2n+1)x)/sinx)dx
et intégrale de 0 à pi de ((x^4)*sin((2n+1)x)/sinx)dx
j'ai essayé de faire une intégration par partie mais je n'y arrive pas.
Est-ce que quelqu'un aurait une idée?
Intégrales
4 messages
- Page 1 sur 1
bonjour,
il suffit de s'inspirer du noyau de Dirichlet:
Avec la formule d'Euler:
x)}{\sin(x)} = \frac{e^{-i((2n+1)x)}-e^{i((2n+1)x)}}{e^{- ix} - e^{ix}}=e^{- 2nix} \quad \frac{1-{(e^{2ix})}^{2n+1}}{1-e^{2ix}})
le facteur de droite est donc la somme des (2n+1) premiers termes d'une suite géométrique. L'intégrale se linéarise en:
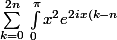} dx)
Il y a le terme central qui donne
et l'on regroupe les autres termes conjugués deux à deux.
Cordialement,
il suffit de s'inspirer du noyau de Dirichlet:
Avec la formule d'Euler:
le facteur de droite est donc la somme des (2n+1) premiers termes d'une suite géométrique. L'intégrale se linéarise en:
Il y a le terme central qui donne
et l'on regroupe les autres termes conjugués deux à deux.
Cordialement,
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
