Enveloppe convexe

[Dyo]

Bonjour,

Quelqu'un pourrait-il me dire comment démontrer ce résultat:
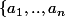
est l'enveloppe convexe de , alors
s'écrit ainsi


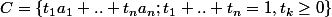
Cette écriture est intuitive pour une enveloppe convexe et pour moi découle de la définition, mais j'aimerais une idée de démonstration rigoureuse.

Merci à vous

[tize]

Bonjour,
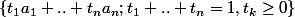
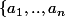
montre que est convexe et que tout convexe qui contient contient .

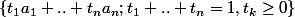
[Dyo]

J'ai pensé à cette méthode mais j'ai un peu de mal pour la deuxième partie

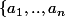
tout convexe qui contient contient

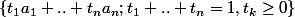
[tize]

Par exemple une petite récurrence :
Si t3=t4=...=tn=0 alors par définition t1a1+t2a2 est dans C avec t1, t2 positifs et t1+t2=1.

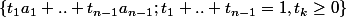
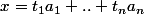
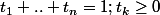
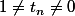
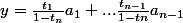
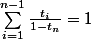
Si est dans C alors pour avec et on a est dans C car et donc est dans C.

[Dyo]

Ok je pensais pas que ca menait à quelque chose la récurrence, merci bien Tize ;)