Une intégrale particulière...

[mathman123]

Bonjour,

Cela fait quelque temps que j'essaie d'étudier les propriétés de cette intégrale à travers des questions proposées par l'énoncé:




1 - Montrer que J est dérivable et que

(à déduire du fait que pour u,v réels, ...)

2 - Montrer que , avec a élément de ]0,Pi/2[ et g une fonction de classe 1 de [0,a] dans . En déduire .


Toute aide ou indication est la bienvenue!! Merci bcp!

[alavacommejetepousse]

bonjour

qu 'as tu fait ?

[rifly01]

Salut,

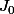
C'est la fonction de Bessel.

[Maxmau]

Bj
pour le 2: essaie une intégration par parties en dérivant g

[mathman123]

bon c finalement bon pour la 1...

pour la 2 je ne comprends pas comment utiliser l'integration par parties...

[Maxmau]

bon c finalement bon pour la 1...

pour la 2 je ne comprends pas comment utiliser l'integration par parties...

Cherche une primitive de t -----> cos(x sint)cost
En intégrant par parties tu vas faire apparaître le x en dénominateur et comme x tend vers infini………..

[mathman123]

Ah oui! mais la déduction alors? j'ai essayé de décomposer l'integrale J mais j'aboutis pas!

[Maxmau]

Ah oui! mais la déduction alors? j'ai essayé de décomposer l'integrale J mais j'aboutis pas!

Après l'IPP
Essaie de majorer la valeur absolue de l'intégrale par quelque chose de la forme C/x

[mathman123]

je ne vois pas l'interet...

[Maxmau]

je ne vois pas l'interet...

Puique tu dois montrer que l'intégrale tend vers zéro lorsque x tend vers +infini

[mathman123]

ah si je prends g = 1/cos ca marche non?

[Maxmau]

ah si je prends g = 1/cos ca marche non?

non car g est donnée quelconque C1 sur l'intervalle

[Maxmau]

Je pose f(t) = sin(x sint)/x (f dépend de x) d’où : f’(t) = cos(x sint)cost
L’intégrale du 2/ s’écrit :
I(x) = Integ( 0 à a ; g(t) f’(t) dt )
Une intégration par parties donne :
I(x) = g(a) f(a) – g(0) f(0) - Integ( 0 à a ; g’(t) f(t) dt ). En mettant 1/x en facteur :
I(x) = (1/x) [g(a) sin(x sina) - Integ( 0 à a ; g’(t) sin(x sint) dt ) ]
Comme le sinus est plus petit que 1 en valeur absolue
|g(a)sin(x sina)| <= |g(a)| et
| Integ( 0 à a ; g’(t) sin(x sint) dt | <= Integ( 0 à a ; |g’(t)| dt )
D’où : |I(x)| <= (1/x) [|g(a)| + Integ( 0 à a ; |g’(t)| dt )]
C’est à dire : : |I(x)| <= C/x où C est indépendant de x
Je te laisse conclure

[Maxmau]

ah si je prends g = 1/cos ca marche non?

Il y a de l'incompréhension dans l'air
Je pensais qu'on était toujours sur le début du 2/ (intégration par parties)
Pour la fin du 2: cette idée est bonne