Bases
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 18:59
par waterproof » 24 Avr 2008, 18:59
bonjour
en fait, j'ai des problèmes pour déterminer les bases de certaines structures alors que ça ne devrait pas poser problème :
par exemple, quelle est une base du plan d'équation x+y+z=0? On est dans un espace de dimension 3, avec pour base orthonormée (i,j,k)
merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 24 Avr 2008, 19:02
par Monsieur23 » 24 Avr 2008, 19:02
Bonjour.
Ton plan est normal au vecteur (1,1,1).
Il te suffit donc de trouver deux vecteurs non colinéaires, orthogonaux à (1,1,1).
« Je ne suis pas un numéro, je suis un homme libre ! »
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 19:09
par waterproof » 24 Avr 2008, 19:09
ok merci pour ton aide
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 19:23
par waterproof » 24 Avr 2008, 19:23
cependant je n'arrive pas à résoudre mon problème :
On a une base (i,j,k) orthonormée de E et on veut la matrice de la projection orthogonale sur le plan P d'équation x+y+z=0
On peut donc dire par exemple que le vecteur t=i+j+k est orthogonal à P, si on note D la droite engendrée par ce vecteur,
donc
 = Id - P_D (x))
avec
 = (x/t)t)
, mais je n'arrive pas à m'en sortir...
comment calculer (x/t) ? je prend quoi pour x?
merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Avr 2008, 19:25
par Nightmare » 24 Avr 2008, 19:25
Salut :happy3:
Simplement :
x=-y-z
Soit (x,y,z) dans ton plan, il s'écrit y(-1,1,0)+z(-1,0,1)
Les vecteurs (-1,1,0) et (-1,0,1) forment une base de ton hyperplan.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 24 Avr 2008, 19:31
par Monsieur23 » 24 Avr 2008, 19:31
Tu veux une matrice, donc tu dois calculer les images de vecteurs de base ( i j et k en l'occurrence ).
« Je ne suis pas un numéro, je suis un homme libre ! »
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 19:35
par waterproof » 24 Avr 2008, 19:35
oui mais en fait mon problème c'est :
 = \sum_{k=1}^n (x/e_k) e_k)
avec P la projection sur le plan P par exemple
Donc la il suffit de calculer :
 = (x/e_1) e_1 + (x/e_2) e_2)
avec
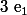
et
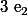
comme tu les as définis, mais après comment je calcule ça? je pose
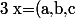)
et je calcule? Comment je remonte ensuite à la matrice?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 24 Avr 2008, 19:40
par Monsieur23 » 24 Avr 2008, 19:40
Attention, c'est la somme des (x / ek) / ||ek||².
Sinon, là c'est bon, maintenant, tu calcules ça pour x=i, x=j et x=k.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 19:52
par waterproof » 24 Avr 2008, 19:52
Monsieur23 a écrit:Attention, c'est la somme des (x / ek) / ||ek||².
Sinon, là c'est bon, maintenant, tu calcules ça pour x=i, x=j et x=k.
donc par exemple pour la première colonne, ça donne :
 = \frac{1}{ \sqrt{2}} (i/e_1) e_1 + \frac{1}{ \sqrt{2}} (i/e_2) e_2)
 e_1 + \frac{1}{ \sqrt{2}} ( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} / <br />\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} ) e_2)

or
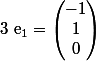
donc
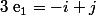
, idem pour
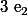
, et donc on a en remplaçant :
 = \sqrt{2} i - \sqrt{2} j)
et donc la première colonne est

c'est ça?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 24 Avr 2008, 20:05
par Monsieur23 » 24 Avr 2008, 20:05
Oué ! C'est ça !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 20:17
par waterproof » 24 Avr 2008, 20:17
ok, mais quand même quelque chose qui me gène :
on peut aussi raisonner par rapport à la projection sur D, droite orthogonale à P, de vecteur directeur
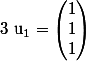
et donc on aurait l'expression de
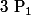
projection orthogonale à P (celle que l'on cherche) telle que :
 = Id - \frac{1}{ 3}(x/u_1) u_1)
donc
= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - \frac{1}{ 3} ( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}) u_1)
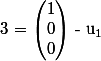
)
donc la première colonne serait

c'est pas la même chose!
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 20:19
par waterproof » 24 Avr 2008, 20:19
waterproof a écrit:donc par exemple pour la première colonne, ça donne :
 = \frac{1}{ \sqrt{2}} (i/e_1) e_1 + \frac{1}{ \sqrt{2}} (i/e_2) e_2)
 e_1 + \frac{1}{ \sqrt{2}} ( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} / <br />\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} ) e_2)

or
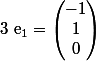
donc
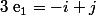
, idem pour
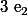
, et donc on a en remplaçant :
 = \sqrt{2} i - \sqrt{2} j)
et donc la première colonne est

c'est ça?
et ici d'ailleurs c'est pas
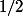
au lieu de
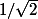
?
bon j'ai compris le problème, je me suis trompé dans les vecteurs on obtient autre chose donc
-
waterproof
- Membre Naturel
- Messages: 19
- Enregistré le: 19 Avr 2008, 12:58
-
 par waterproof » 24 Avr 2008, 20:34
par waterproof » 24 Avr 2008, 20:34
quelqu'un a une explication pourquoi je ne trouve pas la même matrice suivant que je raisonne avec la projection par rapport au plan ou celle par rapport à la droite (Id-projection sur la droite) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
 = Id - P_D (x)) avec
avec  = (x/t)t) , mais je n'arrive pas à m'en sortir...
, mais je n'arrive pas à m'en sortir...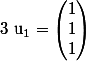 et donc on aurait l'expression de
et donc on aurait l'expression de 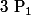 projection orthogonale à P (celle que l'on cherche) telle que :
projection orthogonale à P (celle que l'on cherche) telle que :  = Id - \frac{1}{ 3}(x/u_1) u_1)
= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - \frac{1}{ 3} ( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}) u_1)
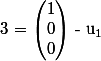
) donc la première colonne serait
donc la première colonne serait  c'est pas la même chose!
c'est pas la même chose!