Suites

[julia1991]

bonjour,

si u(n+1)=u(n)/1-2u(n) comment peut on trouver l'expression de u(n)?

merci

[_-Gaara-_]

Salut,

la question t'es posée telle quelle ou il y a des étapes intermédiaires ?

[tize]

Bonjour,
si tu n'as pas d'indication je te conseille d'étudier la suite

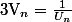
[julia1991]

ben en fait je doit montrer que v(n+1)-v(n) est une constante...

et on sait que u(n+1)=u(n)/1-2u(n) et que v(n)=1/u(n)

[_-Gaara-_]

tu dois trouver que v(n+1) - v(n) = -2 (c'est la raison d'une suite arithmétique si je ne m'abuse)

et en déduire un tas de trucs =) :zen:

[tize]

Oui bah ya plus qu'à...
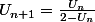
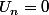
, on inverse (dans le cas où de toute manière si on a 0 alors pour tout ) :

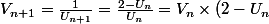[julia1991]

oui mais je suis bloquer a une etape...il faut bien remplacer u(n+1) par sa formule?et u(n) aussi non?

[_-Gaara-_]

Si tu trouves l'expression de V(n) tu trouveras l'expression de 1/U(n) et donc celle de U(n)

et oui

si tu as V(n+1) = 1/U(n+1) donc V(n+1) = 1/u(n)/1-2u(n)

[julia1991]

moi j'arrive a sa:

v(n+1)-v(n)=(1/u(n+1))-(1/u(n))
=(u(n)-u(n+1))/(u(n+1)*u(n))

si c'est sa je fait comment apres?

[_-Gaara-_]

moi j'arrive a sa:

v(n+1)-v(n)=(1/u(n+1))-(1/u(n))
=(u(n)-u(n+1))/(u(n+1)*u(n))

si c'est sa je fait comment apres?

=)

v(n+1)-v(n)=(1/u(n+1))-(1/u(n)) = (1/u(n)/1-2u(n)) - 1/u(n)

= (1-2u(n))/u(n) - 1/u(n)

= -2u(n)/u(n) = -2 :we:

[julia1991]

ha ouai vu comme c'est c'est facile lol merci

[_-Gaara-_]

de rien :we:

[julia1991]

on me demande de calculer u(50) comment on peut faire?

[_-Gaara-_]

on me demande de calculer u(50) comment on peut faire?

as tu trouvé la formule explicite de u(n) en fonction de n ?

[julia1991]

ben je pensais plutot trouver la formule de v(n) en fonction de n pour ensuite appliquer v(n)=1/u(n) non?

[_-Gaara-_]

ben je pensais plutot trouver la formule de v(n) en fonction de n pour ensuite appliquer v(n)=1/u(n) non?

qu'as tu trouvé pour v(n) :we:

[julia1991]

ben j'ai pas encore trouver mais la technique est bonne non?

[_-Gaara-_]

c'est plus simple de faire dans cet ordre :

1 - trouver l'expression de V(n) en fonction de n (tu sais que c'est une suite arithmétique de raison -2...)

2 - en déduire l'expression de U(n) en fonction de n

3 - Calculer u(50)

=)

[julia1991]

oui c'est vrai mais est ce qu'il est possible de trouver l'expression de v(n) en fonction de n pcq moi j'ai du mal...

[julia1991]

ha non non pardon c'est bon je l'ai

v(n)=7*(-2)^n

c'est sa,